
| 身高/cm | 60 | 70 | 80 | 90 | 100 | 110 |
| 体重/kg | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 |
| 身高/cm | 120 | 130 | 140 | 150 | 160 | 170 |
| 体重/kg | 20.02 | 26.86 | 31.11 | 38.85 | 47.25 | 55.05 |
分析 (1)根据表中数据画出散点图,观察发现,这些点的连线是一条向上弯曲的曲线,根据这些点的分布情况,可以考虑用y=a•bx这一函数模型来近似刻画这个地区未成年男性体重y与身高x的函数关系.
2)将x=175代入y=2×1.02x得y=2×1.02175,由计算器可算得y≈63.98,即可得出结论.
解答 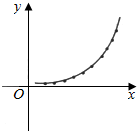 解:(1)以身高为横坐标,体重为纵坐标,画出散点图如图所示,根据点的分布情况,可考虑以y=a•bx作为刻画这个地区未成年男性的体重与身高关系的函数模型.不妨取其中的两组数据(70,7.90),(160,47.25)代入y=a•bx,得7.90=a•b70,47.25=a•b160,用计算器可算得a≈2,b≈1.02.
解:(1)以身高为横坐标,体重为纵坐标,画出散点图如图所示,根据点的分布情况,可考虑以y=a•bx作为刻画这个地区未成年男性的体重与身高关系的函数模型.不妨取其中的两组数据(70,7.90),(160,47.25)代入y=a•bx,得7.90=a•b70,47.25=a•b160,用计算器可算得a≈2,b≈1.02.
∴得到一个函数模型为y=2×1.02x,作出上述函数的图象(图略)之后.可以发现,这个函数模型与已知数据的拟合程度较好,这说明它能较好地反映这个地区未成年男性体重与身高的关系
(2)将x=175代入y=2×1.02x得y=2×1.02175,
由计算器可算得y≈63.98,
由于78÷63.98≈1.22>1.2,所以,这个男性体型偏胖.
点评 本题的解题过程,体现了根据收集到的数据的特点,通过建立函数模型,解决实际问题的基本过程.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{3}}}{4}$ | C. | 1 | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com