
分析 (1)求导数,利用函数f(x)=ax+$\frac{1}{x+b}$(a,b∈Z)在点(2,f(2))处的切线方程为y=3,求出a,b,即可求f(x)的解析式;
(2)利用导数可得切线斜率,根据点斜式可得切线方程,分别联立切线方程与x=1,y=x的方程可得三角形定点,利用三角形面积公式即可得到结论.
解答 解:(1)∵f(x)=ax+$\frac{1}{x+b}$,
∴f′(x)=a+$\frac{-1}{(x+b)^{2}}$,
∵函数f(x)=ax+$\frac{1}{x+b}$(a,b∈Z)在点(2,f(2))处的切线方程为y=3,
∴f′(2)=a-$\frac{1}{(2+b)^{2}}$=0,
∵f(2)=2a+$\frac{1}{2+b}$=3,
∴a=1,b=-1,
∴f(x)=x+$\frac{1}{x-1}$;
(2)f′(3)=1-$\frac{1}{4}$=$\frac{3}{4}$,f(3)=$\frac{7}{2}$,
∴曲线y=f(x)在点(3,f(3))处的切线方程为y-$\frac{7}{2}$=$\frac{3}{4}$(x-3).
切线与直线x=1交点为(1,$\frac{1}{2}$).
切线与直线y=x交点为(5,5).
直线x=1与直线y=x的交点为(1,1).
从而所围三角形的面积为S=$\frac{1}{2}$|$\frac{1}{2}$-1||5-1|=1
点评 本题考查利用导数研究曲线的切线方程,考查学生综合运用知识分析解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是奇函数 | B. | 是偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 是非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 身高/cm | 60 | 70 | 80 | 90 | 100 | 110 |
| 体重/kg | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 |
| 身高/cm | 120 | 130 | 140 | 150 | 160 | 170 |
| 体重/kg | 20.02 | 26.86 | 31.11 | 38.85 | 47.25 | 55.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
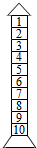 如图是某建筑物的模型,现在要给该模型进行涂色,有红,黄,蓝,绿四种颜色可用,每层只能用一种颜色,在每一层涂色时,每种颜色被使用的可能性相同.
如图是某建筑物的模型,现在要给该模型进行涂色,有红,黄,蓝,绿四种颜色可用,每层只能用一种颜色,在每一层涂色时,每种颜色被使用的可能性相同.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
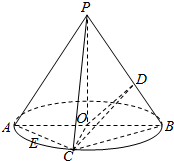 在如图所示的圆锥中,PO是圆锥的高,AB是底面圆的直径,点C是弧AB的中点,E是线段AC的中点,D是线段PB上一点,且PO=2,OB=1.
在如图所示的圆锥中,PO是圆锥的高,AB是底面圆的直径,点C是弧AB的中点,E是线段AC的中点,D是线段PB上一点,且PO=2,OB=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com