
【题目】已知以F为焦点的抛物线C:y2=2px(p>0)上的两点A,B满足 ![]() =3
=3 ![]() ,若弦AB的中点到准线的距离为
,若弦AB的中点到准线的距离为 ![]() ,则抛物线的方程为 .
,则抛物线的方程为 .
【答案】y2=8x
【解析】解:抛物线C:y2=2px的焦点F( ![]() ,0),
,0),
由题意可知直线AB的斜率显然存在,且不为0,设直线AB的方程y=k(x﹣ ![]() ),
),
设A(x1,y1),B(x2,y2),AB的中点M(x,y),
![]() =(
=( ![]() ﹣x1,﹣y1),
﹣x1,﹣y1), ![]() =(x2﹣
=(x2﹣ ![]() ,y2),由
,y2),由 ![]() =3
=3 ![]() ,
,
则 ![]() ﹣x1=3(x2﹣
﹣x1=3(x2﹣ ![]() ),则3x2+x1=2p,①
),则3x2+x1=2p,①
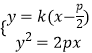 ,整理得:k2x2﹣(k2+2)px+
,整理得:k2x2﹣(k2+2)px+ ![]() =0,
=0,
由韦达定理可知:x1+x2= ![]() ,②x1x2=
,②x1x2= ![]() ,③
,③
由①②解得:x1= ![]() ,x2=
,x2= ![]() ,
,
代入③,解得:k2=3,
则x= ![]() =
= ![]() ,M到准线的距离d=x+
,M到准线的距离d=x+ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,解得:p=4,
,解得:p=4,
∴抛物线的方程为y2=8x.
所以答案是:y2=8x.


科目:高中数学 来源: 题型:
【题目】已知F为双曲线C: ![]() (a>0,b>0)的右焦点,l1 , l2为C的两条渐近线,点A在l1上,且FA⊥l1 , 点B在l2上,且FB∥l1 , 若
(a>0,b>0)的右焦点,l1 , l2为C的两条渐近线,点A在l1上,且FA⊥l1 , 点B在l2上,且FB∥l1 , 若 ![]() ,则双曲线C的离心率为( )
,则双曲线C的离心率为( )
A.![]()
B.![]()
C.![]() 或
或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点A与点A′在x轴上,且关于y轴对称,过点A′垂直于x轴的直线与抛物线y2=2x交于两点B,C,点D为线段AB 上的动点,点E在线段AC上,满足 ![]() .
.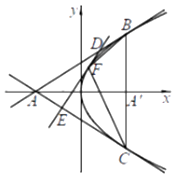
(1)求证:直线DE与此抛物线有且只有一个公共点;
(2)设直线DE与此抛物线的公共点F,记△BCF与△ADE的面积分别为S1、S2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,1),
=(sinx,1), ![]() =(2cosx,3),x∈R.
=(2cosx,3),x∈R.
(1)当 ![]() =λ
=λ ![]() 时,求实数λ和tanx的值;
时,求实数λ和tanx的值;
(2)设函数f(x)= ![]()
![]() ,求f(x)的最小正周期和单调递减区间.
,求f(x)的最小正周期和单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+a)lnx在x=1处的切线方程为y=x﹣1.
(Ⅰ)求a的值及f(x)的单调区间;
(Ⅱ)记函数y=F(x)的图象为曲线C,设点A(x1 , y1),B(x2 , y2)是曲线C上不同的两点,如果在曲线C上存在点M(x0 , y0),使得①x0= ![]() ;②曲线C在点M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.试证明:函数f(x)不存在“中值相依切线”.
;②曲线C在点M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.试证明:函数f(x)不存在“中值相依切线”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如表: 
表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推,例如6613用算筹表示就是: ![]() ,则5288用算筹式可表示为 .
,则5288用算筹式可表示为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆C: ![]() =1(a>b>0),称圆心在原点O,半径为
=1(a>b>0),称圆心在原点O,半径为 ![]() 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F( ![]() ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为 ![]() .
.
(Ⅰ)求椭圆C的方程和其“准圆”方程;
(Ⅱ)点P是椭圆C的“准圆”上的动点,过点P作椭圆的切线l1 , l2交“准圆”于点M,N.
(ⅰ)当点P为“准圆”与y轴正半轴的交点时,求直线l1 , l2的方程并证明l1⊥l2;
(ⅱ)求证:线段MN的长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在正常数a,b,使得x∈R有f(x+a)≤f(x)+b恒成立,则称f(x)为“限增函数”.给出下列三个函数:①f(x)=x2+x+1;② ![]() ;③f(x)=sin(x2),其中是“限增函数”的是( )
;③f(x)=sin(x2),其中是“限增函数”的是( )
A.①②③
B.②③
C.①③
D.③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com