Question

等差数列{a_n}中，a₁＞0，s₄=s₉，则前n项和s_n取最大值时，n为（ ）
A．6
B．7
C．6或7
D．以上都不对

Answer 1

【答案】分析：法一：由a₁＞0，s₄=s₉，结合等差数列的性质可得，a₇=0，从而可得当n=6或n=7时，前n项和s_n取最大
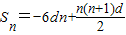
法二：先由题设条件求出a₁=-6d，，然后用配方法进行求解．
解答：解：法一：∵a₁＞0，s₄=s₉，
∴S₉-S₄=a₅+a₆+a₇+a₈+a₉=0
由等差数列的性质可得，5a₇=0，即a₇=0
∵a₁＞0
∴d＜0
当n=6或n=7时，前n项和s_n取最大
故选C
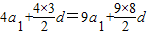
法二：解：由题意可得，，解得a₁=-6d．
∴
=
=，
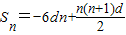
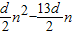
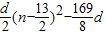
∵a₁＞0，d＜0，
∴当n=6或7时，S_n取最大值-．
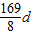
故选C
点评：本题考查等差数列的性质和应用，解题时要注意二次函数配方法的合理运用．