在△ABC中,A,B,C分别是△ABC的三个内角,下列选项中不是“A>B”成立的充要条件的是( )
A.sinA>sinB
B.cosA<cosB
C.tanA>tanB
D.sin2A>sin2B
【答案】
分析:根据三角形内角的取值范围,结合三角函数的性质,利用正弦定理、余弦函数的单调性、举反例题说明等能够求出结果.
解答:解:由正弦定理,得
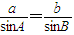
,∴
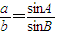
,
∴A>B?a>b(大边对大角)?
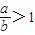
?sinA>sinB(正弦定理),
∴“A>B”成立的充要条件的是sinA>sinB,
故A是“A>B”成立的充要条件;
∵A,B是三角形内角,∴A,B∈(0,π),
∴余弦函数是减函数,
∴A>B?cosA<cosB,
故B是“A>B”成立的充要条件;
∵当A=
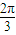
,B=

时,A>B,但tanA=-
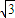
,tanB=
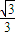
,tanA<tanB,
∴A>B是tanA>tanB的不充分条件
同样当A=
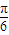
,B=
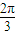
时,tanA>tanB,此时,A<B,
∴A>B是tanA>tanB的不必要条件.
∴“A>B”是“tanA>tanB”成立的既不充分也不必要条件.
故C不是“A>B”成立的充要条件.
∵A,B是三角形内角,∴A,B∈(0,π),
∴sinA>sinB>0,∴sin
2A>sin
2B,
故D是“A>B”成立的充要条件.
故选C.
点评:本题主要考查了充要条件的判断,解决选择题常常采用例举反例的方法进行判定,属于中档题.

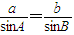 ,∴
,∴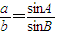 ,
,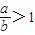 ?sinA>sinB(正弦定理),
?sinA>sinB(正弦定理),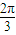 ,B=
,B= 时,A>B,但tanA=-
时,A>B,但tanA=-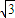 ,tanB=
,tanB=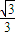 ,tanA<tanB,
,tanA<tanB,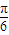 ,B=
,B=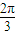 时,tanA>tanB,此时,A<B,
时,tanA>tanB,此时,A<B,
