练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    A是△BCD所在平面外的一点,E,F分别是BC,AD的中点.

    (1)求证:直线EF与BD是异面直线;

    (2)若AC⊥BD,AC=BD,求EF与BD所成的角.


     (1)证明:假设EF与BD不是异面直线,则EF与BD共面,从而DF与BE共面,即AD与BC共面,所以A,B,C,D在同一平面内,这与A是△BCD所在平面外的一点相矛盾,故直线EF与BD是异面直线.

    (2)解:取CD的中点G,连接EG,FG,则EG∥BD,

    所以相交直线EF与EG所成的角,即为异面直线EF与BD所成的角.

    在Rt△EGF中,由EG=FG=AC,求得∠FEG=45°,

    即异面直线EF与BD所成的角为45°.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    当x＞0时， f(x)＝的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某四面体的三视图如图所示.该四面体的六条棱的长度中,最大的是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


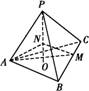
    如图,三棱锥PABC的高PO=8,AC=BC=3,

    ∠ACB=30°,M,N分别在BC和PO上,且CM=x,PN=2CM,则三棱锥NAMC的体积V在x∈(0,3]上的最大体积是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出下列命题,其中正确命题的个数是(　 　)

    ①如果线段AB在平面α内,那么直线AB在平面α内;

    ②两个不同的平面可以相交于不在同一直线上的三个点A、B、C;③若三条直线a,b,c互相平行且分别交直线l于A,B,C三点,则这四条直线共面;④若三条直线两两相交,则这三条直线共面;⑤两组对边相等的四边形是平行四边形.

    (A)1    (B)2    (C)3    (D)4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


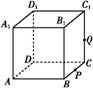
    如图,正方体ABCDA1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是　　　　(写出所有正确命题的编号). 

    ①当0<CQ<时,S为四边形;

    ②当CQ=时,S为等腰梯形;

    ③当CQ=时,S与C1D1的交点R满足C1R=;

    ④当<CQ<1时,S为六边形;

    ⑤当CQ=1时,S的面积为.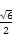

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若α、β是两个相交平面,点A不在α内,也不在β内,则过点A且与α和β都平行的直线(　　)

    (A)只有1条 (B)只有2条

    (C)只有4条 (D)有无数条

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,直三棱柱ABCA1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E.要使AB1⊥平面C1DF,则线段B1F的长为(　 　)

    (A)    (B)1

    (C)    (D)2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线ax＋by＋c＝0与圆O：x2＋y2＝1相交于A，B两点，且|AB|＝，则·的值是(　　)

    A．－  B.

    C．－  D．0

    查看答案和解析>>

    同步练习册答案