
| 年份 | 2004 | 2006 | 2008 | 2010 | 2012 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
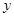 =
=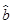 x+
x+
科目:高中数学 来源:不详 题型:解答题
| 甲班: | 158 | 168 | 162 | 168 | 163 | 170 | 182 | 179 | 171 | 179 |
| 乙班: | 159 | 168 | 162 | 170 | 165 | 173 | 176 | 181 | 178 | 179 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.12 | B.20 | C.30 | D.40 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
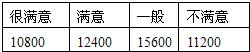
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

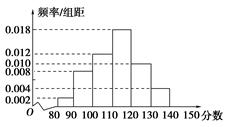
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | | | |
| 女生 | | | |
| 总计 | | | |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
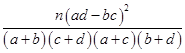 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
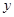 与
与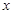 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数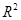 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )A.模型1的相关指数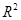 为0.98 为0.98 | B.模型2的相关指数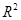 为0.86 为0.86 |
C.模型3的相关指数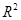 为0.68 为0.68 | D.模型4的相关指数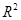 为0.58 为0.58 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.2人 | B.3人 | C.4人 | D.5人 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
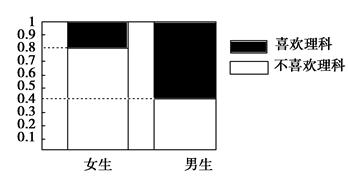
| A.性别与是否喜欢理科无关 |
| B.女生中喜欢理科的比为80% |
| C.男生比女生喜欢理科的可能性大些 |
D.男生中喜欢理科的比为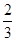 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com