
分析 首先利用双曲线的定义求出关系式,进一步利用均值不等式建立关系式,$\frac{{{{|{P{F_1}}|}^2}}}{{|{P{F_2}}|}}$=$\frac{(2a+n)^{2}}{n}$=4a+$\frac{4{a}^{2}}{n}$+n≥8a,即可求出结果.
解答 解:设|PF2|=n,(n≥c-a),
则:根据双曲线的定义:|PF1|=2a+n,
则:$\frac{{{{|{P{F_1}}|}^2}}}{{|{P{F_2}}|}}$=$\frac{(2a+n)^{2}}{n}$=4a+$\frac{4{a}^{2}}{n}$+n≥8a,
当且仅当n=2a时成立.
所以:c-a≤2a,即c≤3a,
即解得:1<e≤3,
双曲线的离心率的取值范围为:(1,3].
点评 本题考查的知识要点:双曲线的定义的应用.双曲线的离心率,均值不等式的应用,属于中等题型.


科目:高中数学 来源: 题型:解答题
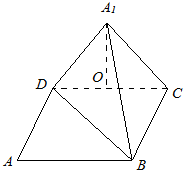 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1O⊥平面BCD.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1O⊥平面BCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分条件但非必要条件 | B. | 必要条件但非充分条件 | ||
| C. | 充分必要条件 | D. | 非充分条件,也非必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com