
| A. | 3 | B. | $2\sqrt{3}$ | C. | $\sqrt{13}$ | D. | $\frac{{12\sqrt{13}}}{13}$ |
分析 由题意直线l:x+my+1=0过圆心C(1,2),从而得到m=-1.圆C半径r=2,当过点M(-1,-1)的切线的斜率不存在时,切线方程为x=-1,把x=-1代入圆C,得P(-1,2);当过点M(-1,-1)的切线的斜率存在时,设切线方程为y=k(x+1)-1,由圆心C(1,2)到切线y=k(x+1)-1的距离d=r,求出切线方程,与圆联立,得Q($\frac{23}{13}$,$\frac{2}{13}$),由此能求出|PQ|.
解答 解:∵圆C:x2+y2-2x-4y+1=0上存在两点关于直线l:x+my+1=0对称,
∴直线l:x+my+1=0过圆心C(1,2),
∴1+2m+1=0.解得m=-1.
圆C:x2+y2-2x-4y+1=0的圆心(1,2),半径r=$\frac{1}{2}\sqrt{4+16-4}$=2,
当过点M(-1,-1)的切线的斜率不存在时,切线方程为x=-1,
圆心C(1,2)到x=-1的距离为2,成立,
把x=-1代入圆C:x2+y2-2x-4y+1=0,得y=2,∴P(-1,2),
当过点M(-1,-1)的切线的斜率存在时,设切线方程为y=k(x+1)-1,
圆心C(1,2)到切线y=k(x+1)-1的距离d=$\frac{|k-2+k-1|}{\sqrt{{k}^{2}+1}}$=$\frac{|2k-3|}{\sqrt{{k}^{2}+1}}=2$,
解得k=$\frac{5}{12}$,
∴切线方程为y=$\frac{5}{12}$(x+1)-1,即5x-12y-7=0,
联立$\left\{\begin{array}{l}{5x-12y-7=0}\\{{x}^{2}+{y}^{2}-2x-4y+1=0}\end{array}\right.$,得169x2-598x+529=0,解得x=$\frac{23}{13}$,y=$\frac{2}{13}$,∴Q($\frac{23}{13}$,$\frac{2}{13}$),
∴|PQ|=$\sqrt{(\frac{23}{13}+1)^{2}+(\frac{2}{13}-2)^{2}}$=$\frac{12\sqrt{13}}{13}$.
故选:D.
点评 本题考查线段长的求法,是中档题,解题时要认真审题,注意圆的性质、点到直线的距离公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20π | B. | 24π | C. | 28π | D. | 32π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 支持 | a= | c= | |
| 不支持 | b= | d= | |
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{13}$ | C. | $\sqrt{15}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
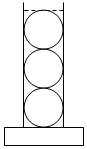 如图,圆柱形容器内盛有高度为6cm的水,若放入3个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,则球的半径为( )
如图,圆柱形容器内盛有高度为6cm的水,若放入3个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,则球的半径为( )| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1 cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com