练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，若(a－c·cos B)·sin B＝(b－c·cos A)·sin A，判断△ABC的形状．

    【答案】△ABC是等腰三角形或直角三角形

    【解析】

    试题先通过正弦定理把a，b，c的表达式代入（a﹣ccosB）sinB=（b﹣ccosA）sinA中，化简整理，进而可推断三角形是等腰或直角三角形．

    试题解析：

    根据正弦定理，原等式可化为：

    (sin A－sin Ccos B)sin B＝(sin B－sin Ccos A)sin A，

    即sin Ccos Bsin B＝sin Ccos Asin A.

    ∵sin C≠0，

    ∴sin Bcos B＝sin Acos A.

    ∴sin 2B＝sin 2A.

    ∴2B＝2A或2B＋2A＝π，

    即A＝B或A＋B＝.

    ∴△ABC是等腰三角形或直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设实数满足，若的最大值为16，则实数__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为F1，F2，过点F1的直线与C交于A，B两点.△ABF2的周长为，且椭圆的离心率为.

    （1）求椭圆C的标准方程：

    （2）设点P为椭圆C的下顶点，直线PA，PB与y＝2分别交于点M，N，当|MN|最小时，求直线AB的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线与坐标轴的交点都在圆C上.

    （1）求圆C的方程；

    （2）若圆C与直线交于A，B两点，且，求a的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在△ABC中，∠B＝，AB＝8，点D在BC边上，CD＝2，cos∠ADC＝.

    （1）求sin∠BAD；

    （2）求BD，AC的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

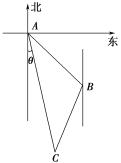
    【题目】如图，甲船在A处，乙船在A处的南偏东45°方向，距A有9海里的B处，并以20海里每小时的速度沿南偏西15°方向行驶，若甲船沿南偏东θ度的方向，并以28海里每小时的速度行驶，恰能在C处追上乙船．问用多少小时追上乙船，并求sin θ的值．(结果保留根号，无需求近似值)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，以坐标原点为中心，以坐标轴为对称轴的帮圆C经过点M（2，1），N.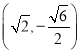

    （1）求椭圆C的标准方程；

    （2）经过点M作倾斜角互补的两条直线，分别与椭圆C相交于异于M点的A，B两点，当△AMB面积取得最大值时，求直线AB的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列的公差不为零，且，、、成等比数列，数列满足

    （1）求数列、的通项公式；

    （2）求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若对任意的实数都有成立，求实数的值；

    （2）若在区间上为单调增函数，求实数的取值范围；

    （3）当时，求函数的最大值.

    查看答案和解析>>

    同步练习册答案