练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．满足不等式lg（x+1）＜lg（3-x）的所有实数x的取值范围是（　　）
    A．（-∞，1）B．（-1，1）C．（-1，3）D．（1，3）

    分析 直接利用对数函数的单调性把对数不等式转化为一元一次不等式组求解．

    解答 解：由lg（x+1）＜lg（3-x），得$\left\{\begin{array}{l}{x+1＞0}\\{3-x＞0}\\{x+1＜3-x}\end{array}\right.$，解得-1＜x＜1．
    ∴实数x的取值范围是（-1，1），
    故选：B．

    点评 本题考查对数不等式的解法，关键是注意要使原对数式有意义，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．已知椭圆的中心在原点，焦点在x轴上，离心率为$\frac{\sqrt{3}}{2}$，且经过点M（4，1）．直线l：y=x+m交椭圆于A，B两不同的点．
    （1）求椭圆方程；
    （2）若直线l与椭圆有两个不同的交点，求m的取值范围；  
    （3）若直线l不过点M，求证：直线MA，MB与x轴围成等腰三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

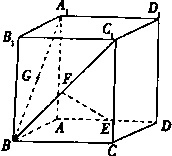    5．如图，在单位正方体A1B1C1D1-ABCD中，E，F，G分别是AD，BC1，A1B的中点．
    （1）求证：EF∥平面C1CDD1；
    （2）求证：EG⊥平面A1BC1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．设集合A={x|y=$\sqrt{2-x}$}，B={y|y=ln（3-x）}，则A∩B（　　）
    A．{x|x≤2}B．{x|x＜3}C．{x|2＜x≤3}D．{x|2≤x＜3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．如图所示：O、A、B是平面上的三点，设向量$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，且|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=2在平面AOB上，若P为线段AB的中垂线上任意一点，则$\overrightarrow{OP}$•（$\overrightarrow{a}$-$\overrightarrow{b}$）的值是（　　）
    A．$\frac{5}{2}$B．5C．3D．$\frac{3}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=lgkx，g（x）=lg（x+1），h（x）=$\frac{x}{{x}^{2}+1}$．
    （1）当k=1时，求函数y=f（x）+g（x）的单调区间；
    （2）若方程f（x）=2g（x）仅有一个实根，求实数k的取值集合；
    （3）设p（x）=h（x）+$\frac{mx}{1+x}$在区间（-1，1）上有且仅有两个不同的零点，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．下列每组表示同一集合的是（　　）
    A．M={2，3}，S={（2，3）}
    B．M={π}，S={3.14}
    C．M={0}，S=∅
    D．M={1，2，3，…，n-1，n}，S={前n个非零自然数}

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．函数y=f（x）+2x是偶函数，g（x）=f（x）+x2，g（1）=3，则g（-1）=-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．在△ABC中，角A，B，C的对边分别为a，b，c，且2cos2$\frac{A-B}{2}$cosB-sin（A-B）sinB+cos（A+C）=-$\frac{3}{5}$，a=4$\sqrt{2}$，b=5，则向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为（　　）
    A．$\frac{{\sqrt{2}}}{2}$B．$-\frac{{\sqrt{2}}}{2}$C．$\frac{3}{5}$D．$-\frac{3}{5}$

    查看答案和解析>>

    同步练习册答案