
函数f(x)=M sin (ωx+φ),(ω>0) 在区间 [ a , b ] 上是增函数,且f(a)=-M,f(b)=M,则函数g(x)=M cos (ωx+φ) 在 [ a , b ] 上( )
A.增函数 B.是减函数 C.可以取最大值M D.可以取最小值-M
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源:2011届高考数学第一轮复习测试题6 题型:044
(理)已知向量m=(sinωx+cosωx,![]() cosωx),n=(cosωx-sinωx,2 sinωx),其中ω>0,函数f(x)=m·n,若f(x)相邻两对称轴间的距离为
cosωx),n=(cosωx-sinωx,2 sinωx),其中ω>0,函数f(x)=m·n,若f(x)相邻两对称轴间的距离为![]() .
.
(1)求ω的值,并求f(x)的最大值及相应x的集合;
(2)在△ABC中,a、b、c分别是A、B、C所对的边,△ABC的面积S=5![]() ,b=4,f(A)=1,求边a的长.
,b=4,f(A)=1,求边a的长.
查看答案和解析>>
科目:高中数学 来源:江西省新余一中2012届高三第六次模拟数学文科试题 题型:044
点M是单位圆O(O是坐标原点)与X轴正半轴的交点,点P在单位圆上,∠MOP=x(0<x<π),![]() =
=![]() +
+![]() 四边形OMQP的面积为S,函数f(x)=
四边形OMQP的面积为S,函数f(x)=![]() ·
·![]() +
+![]() S.
S.
(1)求函数f(x)的表达式及单调递增区间;
(2)在△ABC中,a、b、c分别为角A、B、C的对边,若f(A)=3,b=1,S△ABC=![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f (x)=x2+ax+3,当x∈[-2, 2]时f (x)≥a恒成立,求a的取值范围据统计,某市的工业垃圾若不回收处理,每吨约占地4平方米,2002年,环保部门共回收处理了100吨工业垃圾,且以后垃圾回收处理量每年递增20%(工业垃圾经回收处理后,不再占用土地面积).
(Ⅰ)2007年能回收处理多少吨工业垃圾?(精确到1吨)w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅱ)从2002年到2015年底,可节约土地多少平方米(精确到1m2)
(参考数据:1.24≈2.1 1.55=2.5 1.26=3.0 1.213≈10.7 1.214≈12.8)
查看答案和解析>>
科目:高中数学 来源: 题型:
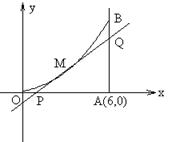
如图所示,曲线段OMB是函数f(x)=x2(0<x<6=的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,⑴试用t表示切线PQ的方程;⑵试用t表示出△QAP的面积g(t);若函数g(t)在(m,n)上单调递减,试求出m的最小值;⑶若S△QAP∈[![]() ],试求出点P横坐标的取值范围
],试求出点P横坐标的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
已知关于x的函数f(x)=![]() +bx2+cx+bc,其导函数为f+(x).令g(x)=∣f (x) ∣,记函数g(x)在区间[-1、1]上的最大值为M.
+bx2+cx+bc,其导函数为f+(x).令g(x)=∣f (x) ∣,记函数g(x)在区间[-1、1]上的最大值为M.
(Ⅰ)如果函数f(x)在x=1处有极值-![]() ,试确定b、c的值:
,试确定b、c的值:
(Ⅱ)若∣b∣>1,证明对任意的c,都有M>2: w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅲ)若M≧K对任意的b、c恒成立,试求k的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com