
| x | 1 | 2 | 3 | 4 | 5 |
| y | 3 | 5 | 7 | 10 | 11 |
分析 (1)由题意,计算样本数据的平均值,求出对应回归直线方程的系数即可;
(2)根据回归直线方程中$\stackrel{∧}{b}$>0,判断是正相关,利用回归方程计算x=10时$\stackrel{∧}{y}$的值即可.
解答 解:(1)由题意:n=5,
计算$\overline x=\frac{1}{5}\sum_{i=1}^5{{x_i}=3}$,
$\overline y=\frac{1}{5}\sum_{i=1}^5{{y_i}=7.2}$,
又$\sum_{i=1}^{5}$${{x}_{i}}^{2}$-5${\overline{x}}^{2}$=55-5×9=10,
$\sum_{i=1}^5{{x_i}{y_i}-5\overline{xy}=129-5×3×7.2=21}$;
∴$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline{xy}}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}=\frac{21}{10}=2.1$,
$\widehata=\overline y-b\overline x=7.2-2.1×3=0.9$,
即所求的回归方程为$\widehaty=2.1x+0.9$;
(2)由于变量y的值随温度x的值增加而增加($\stackrel{∧}{b}$=2.1>0),
∴x与y之间是正相关关系;
当x=10时,$\stackrel{∧}{y}$=2.1×10+0.9=21.9,
即预测当温度达到10°时反应结果为21.9.
点评 本题考查了线性回归方程的求法与应用问题,是基础题目.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:解答题
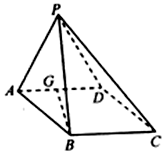 如图所示,在四棱锥P-ABCD中,G为AD的中点,侧面PAD⊥底面ABCD.底面ABCD是边长为a的菱形,且∠D A B=60°,侧面PAD为正三角形.求证:AD⊥平面PGB.
如图所示,在四棱锥P-ABCD中,G为AD的中点,侧面PAD⊥底面ABCD.底面ABCD是边长为a的菱形,且∠D A B=60°,侧面PAD为正三角形.求证:AD⊥平面PGB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2)>f(2m)>f(log2m) | B. | f(log2m)>f(2m)>f(2) | C. | f(2m)>f(log2m)>f(2) | D. | f(2m)>f(2)>f(log2m) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com