搜索
【题目】已知函数
的图象如图所示，则
的取值范围是( )
A. 
B. 
C. 
D. 
参考答案：
【答案】D
【解析】由图象可知：经过原点,∴f(0)=0=d，
∴
.
由图象可得：函数f(x)在[1,1]上单调递减,函数f(x)在x=1处取得极大值。
∴f′(x)=3ax2+2bx+c0在[1,1]上恒成立,且f′(1)=0.
得到3a2b+c=0，即c=2b3a，
∵f′(1)=3a+2b+c<0，
∴4b<0，即b<0，
∵f′(2)=12a+4b+c>0，
∴3a+2b>0，
设k=
,则k=
，
建立如图所示的坐标系,则点A(1,2)，
则k=
式中变量a、b满足下列条件
，
作出可行域如图：
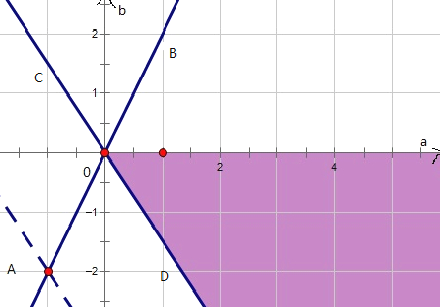
∴k的最大值就是kAB=
,k的最小值就是kCD,而kCD就是直线3a+2b=0的斜率,kCD=
，
∴
<k<
.
∴故选D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校举行汉字听写比赛，为了了解本次比赛成绩情况，从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数，满分100分)进行统计，请根据频率分布表中所提供的数据，解答下列问题：
组号
分组
频数
频率
第1组
[50，60)
5
0.05
第2组
[60，70)
0.35
第3组
[70，80)
30
第4组
[80，90)
20
0.20
第5组
[90，100]
10
0.10
合计
100
1.00
（Ⅰ）求
的值；（Ⅱ）若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛，并从中选出2人做种子选手，求2人中至少有1人是第4组的概率。
-
科目： 来源： 题型：
查看答案和解析>>【题目】在投掷骰子试验中，根据向上的点数可以定义许多事件，如：A={出现1点}，B={出现3点或4点}，C={出现的点数是奇数}，D={出现的点数是偶数}.
(1)说明以上4个事件的关系.
(2)求两两运算的结果.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场有奖销售中，购满100元商品得1张奖券，多购多得.1 000张奖券为一个开奖单位，设特等奖1个，一等奖10个，二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A，B，C，求：
(1)P(A)，P(B)，P(C).
(2)1张奖券的中奖概率.
(3)1张奖券不中特等奖，且不中一等奖的概率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，P是直线x=4上一动点，以P为圆心的圆Γ经定点B（1，0），直线l是圆Γ在点B处的切线，过A（﹣1，0）作圆Γ的两条切线分别与l交于E，F两点．
（1）求证：|EA|+|EB|为定值；
（2）设直线l交直线x=4于点Q，证明：|EB||FQ|=|BF|EQ|．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设函数f（x）=
，g（x）=a（x+b）（0＜a≤1，b≤0）．（1）讨论函数y=f（x）g（x）的奇偶性；
（2）当b=0时，判断函数y=
在（﹣1，1）上的单调性，并说明理由；（3）设h（x）=|af2（x）﹣
|，若h（x）的最大值为2，求a+b的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
。（Ⅰ）求函数
的单调区间；（Ⅱ）若函数
在
上是减函数，求实数
的取值范围。
相关试题
