
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若![]() ,
, ![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,且方程
,且方程![]() 在
在![]() 内有解,求实数
内有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .(2)
.(2)![]()
【解析】【试题分析】(1)先求出函数解析式导数,再借助导数与函数的单调性的关系求解;(2)依据题设先将问题进行等价转化,再构造函数运用导数与函数的单调性的关系研究函数的图像的形状分析求解:
(1)若![]() ,
, ![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
,
①若![]() ,即
,即![]() 时,
时, ![]() ,此时函数单调递减,单调递减区间为
,此时函数单调递减,单调递减区间为![]() ;
;
②若![]() ,即
,即![]() 时,由
时,由![]() ,得
,得![]() ;由
;由![]() 得
得![]() ,或
,或![]() ,
,
所以单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)若![]() ,∴
,∴![]() ,
, ![]() 则,
则,
若方程![]() 在
在![]() 内有解,即
内有解,即![]() 在
在![]() 内有解,
内有解,
即![]() 在
在![]() 有解.
有解.
设![]() ,则
,则![]() 在
在![]() 内有零点,设
内有零点,设![]() 是
是![]() 在
在![]() 内的一个零点,
内的一个零点,
因为![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 和
和![]() 上不可能单调,
上不可能单调,
由![]() ,设
,设![]() ,则
,则![]() 在
在![]() 和
和![]() 上存在零点,
上存在零点,
即![]() 在
在![]() 上至少有两个零点,因为
上至少有两个零点,因为![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上递增,不合题意;
上递增,不合题意;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上递减,不合题意;
上递减,不合题意;
当![]() 时,令
时,令![]() ,得
,得![]() ,则
,则![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
![]() 在
在![]() 上存在最小值
上存在最小值![]() .
.
若![]() 有两个零点,则有
有两个零点,则有![]() ,
, ![]() .
.
所以![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 递增;
递增;
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 递减,
递减,
则![]() ,所以
,所以![]() 恒成立.
恒成立.
由![]() ,
, ![]() ,所以
,所以![]() ,
,
当![]() 时,设
时,设![]() 的两个零点为
的两个零点为![]() ,
,
则![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
则![]() ,
, ![]() ,则
,则![]() 在
在![]() 内有零点,
内有零点,
综上,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个学生在一次竞赛中要回答![]() 道题是这样产生的:从
道题是这样产生的:从![]() 道物理题中随机抽取
道物理题中随机抽取![]() 道;从
道;从![]() 道化学题中随机抽取
道化学题中随机抽取![]() 道;从
道;从![]() 道生物题中随机抽取
道生物题中随机抽取![]() 道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为
道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为![]() ,化学题的编号为
,化学题的编号为![]() ,生物题的编号为
,生物题的编号为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() :
: ![]() ,长轴的右端点与抛物线
,长轴的右端点与抛物线![]() :
: ![]() 的焦点
的焦点![]() 重合,且椭圆
重合,且椭圆![]() 的离心率是
的离心率是![]() .
.
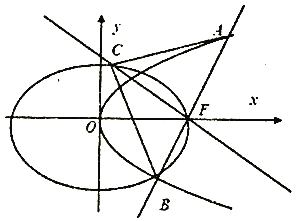
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
, ![]() 两点,过
两点,过![]() 且与直线
且与直线![]() 垂直的直线交椭圆
垂直的直线交椭圆![]() 于另一点
于另一点![]() ,求
,求![]() 面积的最小值,以及取到最小值时直线
面积的最小值,以及取到最小值时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com