
【题目】已知函数![]() ,
,![]() .
.
(1)![]() 恒成立的实数
恒成立的实数![]() 的最大值
的最大值![]() ;
;
(2)设![]() ,
,![]() ,且满足
,且满足![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)化为分段函数,根据函数单调性即可求出函数的最小值,即可求出![]() 的值,
的值,
(2)由m>0,n>0,且![]() ,即:
,即:![]() ,化简
,化简![]()
![]() ≥2|m+2n|,由2|m+2n|=2(m+2n)=2(m+2n)
≥2|m+2n|,由2|m+2n|=2(m+2n)=2(m+2n)![]() (
(![]() )
)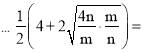 4即可证得.
4即可证得.
(1)已知函数![]() ,
,![]() .由题意得,
.由题意得,![]() 恒成立,
恒成立,
即h(x)=![]() =2|x﹣1|﹣|x+1|=
=2|x﹣1|﹣|x+1|=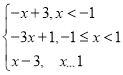 ,
,
显然,h(x)在(﹣∞,1]上单调递减,在(1,+∞)上单调递增,
∴h(x)min=h(1)=﹣2,∴t![]() ﹣2,即最大值
﹣2,即最大值![]() =-2.
=-2.
(2)由于m>0,n>0,且![]() ,即:
,即:![]() ,
,
![]()
![]() =
=![]() +
+![]() =2(|m+1|+|2n﹣1|)≥2|m+2n|,
=2(|m+1|+|2n﹣1|)≥2|m+2n|,
∴2|m+2n|=2(m+2n)=2(m+2n)![]() (
(![]() )
)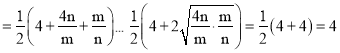 ,
,
当且仅当![]() ,即当n=
,即当n=![]() ,m=
,m=![]() 时取“=”,
时取“=”,
故![]()


科目:高中数学 来源: 题型:
【题目】某城市自2014年至2019年每年年初统计得到的人口数量如表所示.
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数(单位:万) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)设第![]() 年的人口数量为
年的人口数量为![]() (2014年为第1年),根据表中的数据,描述该城市人口数量和2014年至2018年每年该城市人口的增长数量的变化趋势;
(2014年为第1年),根据表中的数据,描述该城市人口数量和2014年至2018年每年该城市人口的增长数量的变化趋势;
(2)研究统计人员用函数![]() 拟合该城市的人口数量,其中
拟合该城市的人口数量,其中![]() 的单位是年.假设2014年初对应
的单位是年.假设2014年初对应![]() ,
,![]() 的单位是万.设
的单位是万.设![]() 的反函数为
的反函数为![]() ,求
,求![]() 的值(精确到0.1),并解释其实际意义.
的值(精确到0.1),并解释其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上任意一点,
上任意一点,![]() ,且点
,且点![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若![]() 为点
为点![]() 关于原点
关于原点![]() 的对称点,过
的对称点,过![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 、
、![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于点
于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生鲜批发店每天从蔬菜生产基地以5元/千克购进某种绿色蔬菜,售价8元/千克,若每天下午4点以前所购进的绿色蔬菜没有售完,则对未售出的绿色蔬菜降价处理,以3元/千克出售.根据经验,降价后能够把剩余蔬菜全部处理完毕,且当天不再进货.该生鲜批发店整理了过往30天(每天下午4点以前)这种绿色蔬菜的日销售量(单位:千克)得到如下统计数据(视频率为概率)(注:x,y∈N*)
每天下午4点前销售量 | 350 | 400 | 450 | 500 | 550 |
天数 | 3 | 9 | x | y | 2 |
(1)求在未来3天中,至少有1天下午4点前的销售量不少于450千克的概率.
(2)若该生鲜批发店以当天利润期望值为决策依据,当购进450千克比购进500千克的利润期望值大时,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,EA⊥平面ABCD,四边形ABCD为等腰梯形,![]() ,且
,且![]() ,AD=AE=1,∠ABC=60°,EF=
,AD=AE=1,∠ABC=60°,EF=![]() AC,且EF
AC,且EF![]() AC.
AC.
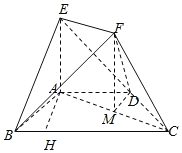
(Ⅰ)证明:AB⊥CF;
(Ⅱ)求二面角B﹣EF﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象关于直线
,其图象关于直线![]() 对称,为了得到函数
对称,为了得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上的所有点( )
的图象上的所有点( )
A.先向左平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
B.先向右平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
C.先向右平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
D.先向左平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ),点
),点![]() 在
在![]() 的焦点
的焦点![]() 的右侧,且
的右侧,且![]() 到
到![]() 的准线的距离是
的准线的距离是![]() 到
到![]() 距离的3倍,经过点
距离的3倍,经过点![]() 的直线与抛物线
的直线与抛物线![]() 交于不同的
交于不同的![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,经过点
,经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求抛物线![]() 的方程和
的方程和![]() 的坐标;
的坐标;
(2)判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)椭圆![]() 的两焦点为
的两焦点为![]() 、
、![]() ,在椭圆
,在椭圆![]() 外的抛物线
外的抛物线![]() 上取一点
上取一点![]() ,若
,若![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com