
 ,BD=DC=CB=2,二面角A-BC-D的平面角等于150°,则该球的表面积为
,BD=DC=CB=2,二面角A-BC-D的平面角等于150°,则该球的表面积为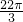
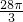
 ,BD=DC=CB=2,设等边△BDC的外接圆的圆心为E,BC中点为H,球心为O,设球半径为r,则由题设条件能够推导出
,BD=DC=CB=2,设等边△BDC的外接圆的圆心为E,BC中点为H,球心为O,设球半径为r,则由题设条件能够推导出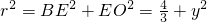 ,且
,且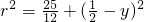 ,由此解得y=1,从而求出r,由此能够求出球的表面积.
,由此解得y=1,从而求出r,由此能够求出球的表面积.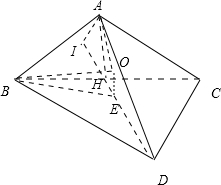 解:由题设知四面体ABCD中,AB=AC=
解:由题设知四面体ABCD中,AB=AC= ,BD=DC=CB=2,
,BD=DC=CB=2, ,
,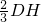 =
=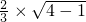 =
= ,HE=
,HE=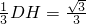 ,
,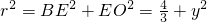 ,…①
,…① ,OA=r,∠AHT=180°-∠AHE=30°,
,OA=r,∠AHT=180°-∠AHE=30°, ,IE=IH+HE=
,IE=IH+HE=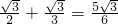 ,
,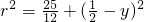 ,…②
,…②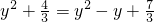 ,解得y=1,
,解得y=1,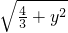 =
= ,
,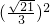 =
=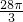 .
.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com