Question

【题目】已知A是抛物线E：y2＝2px(p>0)上的一点，以点A和点B(2,0)为直径两端点的圆C交直线x＝1于M，N两点.

（1）若|MN|＝2，求抛物线E的方程；

（2）若0＜p＜1，抛物线E与圆(x﹣5)2+y2=9在x轴上方的交点为P，Q，点G为PQ的中点，O为坐标原点，求直线OG斜率的取值范围.

Answer 1

【答案】（1）.（2）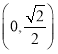

【解析】

（1）设A的坐标为A（x0，y0），由题意可得圆心C的坐标，求出C到直线x＝1的距离.由半个弦长，圆心到直线的距离及半径构成直角三角形可得p的值，进而求出抛物线的方程；

（2）将抛物线的方程与圆的方程联立可得韦达定理，进而求出中点G的坐标，再求出直线OG的斜率的表达式，换元可得斜率的取值范围.

（1）设A（x0，y0）且y02＝2px0，则圆心C（），

圆C的直径|AB|，

圆心C到直线x＝1的距离d＝|1|＝||，

因为|MN|＝2，所以（）2+d2＝（）2，即1，y02＝2px0，

整理可得（2p﹣4）x0＝0，所以p＝2，

所以抛物线的方程为：y2＝4x；

（2）联立抛物线与圆的方程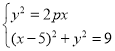整理可得x2﹣2（5﹣p）x+16＝0，△＞0，

设P（x1，y1），Q（x2，y2），则x1+x2＝2（5﹣p），x1x2＝16，

所以中点G的横坐标xG＝5﹣p，yG（），

所以kOG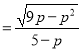（0＜P＜1），

令t＝5﹣p（t∈（4，5）），则kOG（），

解得0＜kOG，

所以直线OG斜率的取值范围（0，）.