
 如图所示,PA⊥平面ABCD,底面ABCD为菱形,$∠ABC=\frac{π}{3}$,PA=AB=4,AC交BD于O,点N是PC的中点.
如图所示,PA⊥平面ABCD,底面ABCD为菱形,$∠ABC=\frac{π}{3}$,PA=AB=4,AC交BD于O,点N是PC的中点.分析 (1)只需证明BD⊥AC,BD⊥PA,即可得到BD⊥平面PAC.
(2)以O为坐标原点,OC,OB,ON所在直线分别为x,y,z轴,求出两平面的法向量,利用向量的夹角公式求解.
解答 解:(1)∵ABCD是菱形,∴BD⊥AC,
又∵PA⊥平面ABCD,BD?平面ABCD,∴BD⊥PA,
而PA∩AC=A,
∴BD⊥平面PAC.
(2)以O为坐标原点,OC,OB,ON所在直线分别为x,y,z轴,方向如图所示,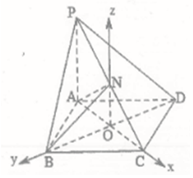
根据条件有点$N(0,0,2),A(-2,0,0),B(0,2\sqrt{3},0)$,
由(1)可知OB⊥平面ANC,所以可取$\overrightarrow{OB}$为平面ANC的法向量$\overrightarrow{n_1}$,$\overrightarrow{n_1}=\overrightarrow{OB}=(0,2\sqrt{3},0)$,
现设平面BAN的法向量为$\overrightarrow{n_2}=(x,y,z)$,则有$\left\{\begin{array}{l}\overrightarrow{AN}•\overrightarrow{n_2}=0\\ \overrightarrow{BN}•\overrightarrow{n_2}=0\end{array}\right.$$⇒\left\{\begin{array}{l}x+z=0\\-\sqrt{3}y+z=0\end{array}\right.$,
令z=1,
则$\overrightarrow{n_2}=(-1,\frac{{\sqrt{3}}}{3},1)$,
设平面ANC与平面ANB所成的锐二面角大小为θ,则$cosθ=|\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|\overrightarrow{n_1}|•|\overrightarrow{n_2}|}}|=\frac{{\sqrt{7}}}{7}$.
点评 本题考查了空间线面垂直,即向量法求解二面角,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:解答题
 如图,已知向量$\overrightarrow{AB}=({6,1}),\overrightarrow{BC}=({x,y}),\overrightarrow{CD}=({-2,-3})$.
如图,已知向量$\overrightarrow{AB}=({6,1}),\overrightarrow{BC}=({x,y}),\overrightarrow{CD}=({-2,-3})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
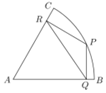 如图,扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条商业街道,要求街道PQ与AB垂直,街道PR与AC垂直,线段RQ表示第三条街道.
如图,扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条商业街道,要求街道PQ与AB垂直,街道PR与AC垂直,线段RQ表示第三条街道.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
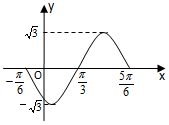 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期上的图象如图所示,
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期上的图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com