
有一个正四面体的棱长为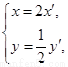 ,现用一张圆形的包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小半径为 .
,现用一张圆形的包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小半径为 .
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:重庆市37中2005-2006年高二下第一次月考数学试题 题型:013
有一个正四面体的木块,棱长为a.一只蚂蚁从底面三角形的垂心沿着表面到达顶点,那么它行走路线的最小路程为
A.a
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.五面体 | B.七面体 | C.九面体 | D.十一面体 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com