
已知侧棱垂直于底面的四棱柱,ABCD-A1B1C1D1的底面是菱形,且AD="A" A1,
点F为棱BB1的中点,点M为线段AC1的中点.
(1)求证: MF∥平面ABCD
(2)求证:平面AFC1⊥平面ACC1A1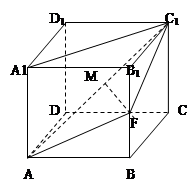
(1)证明见解析;(2)证明见解析.
解析试题分析:
解题思路:(1)构造三角形,利用中位线证明线线平行,再利用线面平行的判定定理证明线面平行;
(2)由线面垂直得到线线垂直,再证明线面垂直,进而证明面面垂直.
规律总结:对于空间几何体中的垂直、平行关系的判定,要牢牢记住并灵活进行转化,线线关系是关键.
试题解析:(1)延长C1F交CB的延长线于点N,连接AN.
∵F是BB1的中点,∴F为C!N的中点,B为CN的中点,
∴又因为M为线段AC!的中点,∴MF∥AN,
又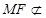 平面ABCD,
平面ABCD,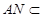 平面ABCD,
平面ABCD,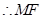 ∥平面ABCD.
∥平面ABCD.
连接BD,由题知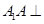 平面AB-CD,又
平面AB-CD,又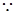
 平面ABCD,
平面ABCD,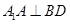 .
.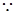 四边形ABCD为菱形,
四边形ABCD为菱形,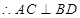 .
.
又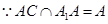 ,
,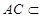 平面
平面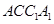 ,
,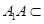 平面
平面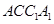 ,
,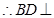 平面
平面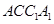 .
.
在四边形DANB中,DA∥BN,且DA=BN,, 四边形DANB为平行四边形,
四边形DANB为平行四边形,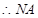 ∥BD,
∥BD,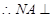 平面
平面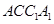 。又
。又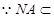 平面
平面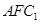 ,
,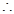 平面
平面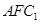 ⊥平面
⊥平面 .
.
考点:1.线面平行的判定定理;2.面面垂直的判定定理.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:解答题
在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点,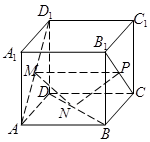
求证:(1)MN∥平面CC1D1D. (2)平面MNP∥平面CC1D1D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图1,在直角梯形 中,
中,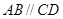 ,
,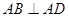 ,且
,且 .现以
.现以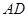 为一边向形外作正方形
为一边向形外作正方形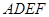 ,然后沿边
,然后沿边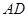 将正方形
将正方形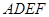 翻折,使平面
翻折,使平面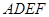 与平面
与平面 垂直,
垂直, 为
为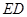 的中点,如图2.
的中点,如图2.
(1)求证: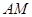 ∥平面
∥平面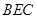 ;
;
(2)求证: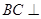 平面
平面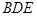 ;
;
(3)求点 到平面
到平面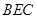 的距离.
的距离.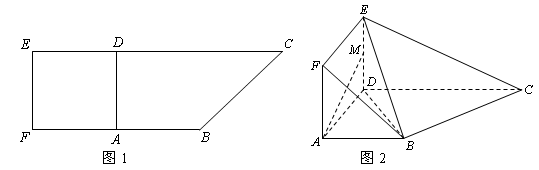
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知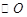 的直径AB=3,点C为
的直径AB=3,点C为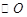 上异于A,B的一点,
上异于A,B的一点,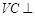 平面ABC,且VC=2,点M为线段VB的中点.
平面ABC,且VC=2,点M为线段VB的中点.
(1)求证: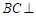 平面VAC;
平面VAC;
(2)若AC=1,求直线AM与平面VAC所成角的大小.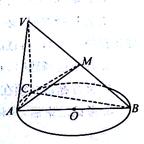
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知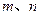 是不同的直线,
是不同的直线,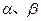 是不重合的平面,给出下列命题:
是不重合的平面,给出下列命题:
①若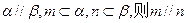
②若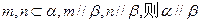
③若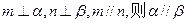
④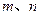 是两条异面直线,若
是两条异面直线,若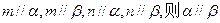
上述命题中,真命题的序号是______________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设 是两条不同的直线,
是两条不同的直线,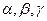 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若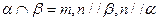 ,则
,则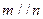 ;
;
②若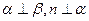 ,则
,则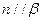 ;
;
③若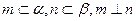 ,则
,则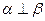 ;
;
④若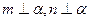 ,则
,则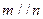 ;
;
其中正确命题有_____________.(填上你认为正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设α、β、γ为彼此不重合的三个平面,ι为直线,给出下列命题:
①若α∥β,α⊥γ,则β⊥γ,
②若α⊥γ,β⊥γ,且αnβ=ι,则ι⊥γ
③若直线l与平面α内的无数条直线垂直则直线ι与平而α垂直,
④若α内存在不共线的三点到β的距离相等.则平面α平行于平面β
上面命题中,真命题的序号为 (写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com