Question

11．某人上午7时，乘摩托艇以匀速vkm/h（8≤v≤40）从A港出发到距100km的B港去，然后乘汽车以匀速wkm/h（30≤w≤100）自B港向距300km的C市驶去．应该在同一天下午4至9点到达C市． 设乘坐汽车、摩托艇去目的地所需要的时间分别是xh，yh．
（1）作图表示满足上述条件的x，y范围；
（2）如果已知所需的经费p=100+3（5-x）+2（8-y）（元），那么v，w分别是多少时p最小？此时需花费多少元？

Answer 1

分析 （1）由路程，速度，时间的关系得出x，y与v，w的关系式，由v，w得范围即可得x，y的范围，再由到达时间范围即可得到不等式组，作图即可；
（2）利用线性规划知识易求．

解答 解：（1）依题意得 $y=\frac{100}{v}，x=\frac{300}{w}，8≤v≤40，30≤w≤100$，∴$3≤x≤10，\frac{5}{2}≤y≤\frac{25}{2}$①
由于乘汽车、摩托艇所需的时间和x+y应在9至 14个小时之间，即9≤x+y≤14②
因此，满足①②的点（x，y）的存在范围是图中阴影部分（包括边界）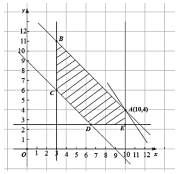

（2）∵p=100+3（5-x）+2（8-y）=131-3x-2y，上式表示斜率为$-\frac{3}{2}$的直线，
当动直线p=131-3x-2y通过图中的阴影部分区域（包括边界），通过点A时，p值最小．
由$\left\{\begin{array}{l}x+y=14\\ x=10\end{array}\right.$得$\left\{\begin{array}{l}x=10\\ y=4\end{array}\right.$，即当x=10，y=4时，p最小． 
此时，v=25，w=30，p的最小值为 93元．

点评 本题考查简单的线性规划的实际运用．正确建立不等式组，把实际问题转化为数学问题是解题关键．属于基础题．