
分析 (1)去掉绝对值符合,即可求函数f(x)的最值;
(2)若?x∈R,f(x)≥t2-$\frac{7}{2}$t恒成立,则-3≥t2-$\frac{7}{2}$t,即可求实数t的取值范围.
解答 解:(1)x<2时,f(x)=-x+2+x-5=-3,
2≤x≤5时,f(x)=x-2+x-5=2x-7∈[-3,3],
x>5时,f(x)=x-2-x+5=3,
∴f(x)的最小值为-3,最大值为3;
(2)∵?x∈R,f(x)≥t2-$\frac{7}{2}$t恒成立,
∴-3≥t2-$\frac{7}{2}$t,
∴(t-2)(2t-3)≤0,
∴$\frac{3}{2}$≤t≤2.
点评 本题考查绝对值不等式,考查恒成立问题,考查学生的计算能力,正确求出函数的最值是关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
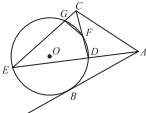 如图,AB是⊙O的一条切线,切点为B,直线ADE、CFD、CGE都是⊙O的割线,已知AC=AB.
如图,AB是⊙O的一条切线,切点为B,直线ADE、CFD、CGE都是⊙O的割线,已知AC=AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com