Question

9．已知三被锥S-ABC的体积为$\frac{4\sqrt{5}}{3}$，底面△ABC是边长为2的正三角形，且所有頂点都在直径为SC的球面上．则此球的半径为2$\sqrt{2}$．

Answer 1

分析 设球心为O，球的半径为R，过ABC三点的小圆的圆心为O₁，则OO₁⊥平面ABC，作SD⊥平面ABC交CO₁的延长线与D，用半径表示出OO₁、高SD，利用V_{三棱锥S-ABC}=$\frac{4\sqrt{5}}{3}$求出R的值．

解答 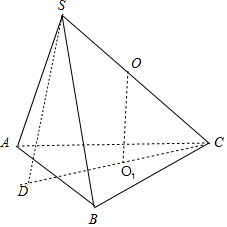解：设球心为O，球的半径为R，
过ABC三点的小圆的圆心为O₁，则OO₁⊥平面ABC，
作SD⊥平面ABC交CO₁的延长线与D，如图所示；
∵△ABC是正三角形，
∴CD=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$，O₁C=$\frac{2}{3}$CD=$\frac{2\sqrt{3}}{3}$，
∴OO₁=$\sqrt{{R}^{2}-\frac{4}{3}}$，
∴高SD=2OO₁=2$\sqrt{{R}^{2}-\frac{4}{3}}$；
又△ABC是边长为2的正三角形，
∴S_△ABC=$\frac{\sqrt{3}}{4}$•2²=$\sqrt{3}$，
∴V_{三棱锥S-ABC}=$\frac{1}{3}$•$\sqrt{3}$•2$\sqrt{{R}^{2}-\frac{4}{3}}$=$\frac{4\sqrt{5}}{3}$，
解得R=2$\sqrt{2}$．
故答案为：2$\sqrt{2}$．

点评 本题考查了棱锥的体积，球内接多面体的应用问题，解题的关键是确定点S到平面ABC的距离，属于中档题．