
分析 (1)根据-π<x<0,判断sinx、cosx的值的正负,sin2x+cos2x=1,即可计算.
(2)根据sinx、cosx的值带入,即可求解.
解答 解:∵-π<x<0,
当$-π<x≤-\frac{π}{2}$时,
可知sinx<0、cosx<0.
∴sinx+cosx=$\frac{1}{5}$不成立.
当$-\frac{π}{2}$<x<0时,
可知sinx<0、cosx>0.
∵sinx+cosx=$\frac{1}{5}$,sin2x+cos2x=1.
∴sinx=$-\frac{3}{5}$,cosx=$\frac{4}{5}$.tanx=$\frac{sinx}{cosx}=-\frac{3}{4}$.
(1)sinx-cosx=$-\frac{3}{5}-\frac{4}{5}=-\frac{7}{5}$.
(2)$\frac{{2{{sin}^2}x+2sinx•cosx}}{1-tanx}$=$\frac{2×\frac{9}{25}-2×\frac{3}{5}×\frac{4}{5}}{1+\frac{3}{4}}$=$-\frac{24}{175}$.
点评 本题考查了同角三角函数基本关系式,考查了计算能力,属于基础题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | d>$\frac{8}{3}$ | B. | d<3 | C. | $\frac{8}{3}$≤d<3 | D. | $\frac{4}{3}$<d≤$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{15}$ | B. | $\frac{11}{15}$ | C. | $\frac{5}{3}$ | D. | $\frac{64}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7π}{4}$ | B. | 2π | C. | $\frac{9π}{4}$ | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
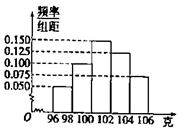 某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),(104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),(104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )| A. | 90 | B. | 75 | C. | 60 | D. | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com