
分析 (1)根据极坐标方程求出直角坐标方程和普通方程即可;(2)根据三角函数的性质求出m的范围即可.
解答 解:(1)由直线l的极坐标方程得:$\sqrt{2}ρ({sinθcos\frac{π}{4}-cosθsin\frac{π}{4}})=m$,
即直线l的直角坐标方程为:y-x=m,
由曲线C的参数方程 $\left\{\begin{array}{l}x=\sqrt{3}cosα\\ y=sinα\end{array}\right.(α$为参数,且α∈[0,π]).
得:${({\frac{x}{{\sqrt{3}}}})^2}+{y^2}=\frac{x^2}{3}+{y^2}=1,y∈[{0,1}]$
(2)设曲线C上任意一点为$({\sqrt{3}cosα,sinα})$,
则$m=sinα-\sqrt{3}cosα=2sin({α-\frac{π}{3}}),α∈[{0,π}]$,
∴-$\frac{π}{3}$≤α-$\frac{π}{3}$≤$\frac{2π}{3}$,
画出y=2sin(α-$\frac{π}{3}$)的图象,如图示: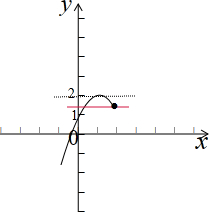 ,
,
α=$\frac{2}{3}$π时,y=2sin$\frac{2}{3}$π=$\sqrt{3}$,
∵直线l与曲线C有两个公共点,结合图象,
∴$m∈[{\sqrt{3},2})$.
点评 本题考查极坐标与参数方程与直角坐标方程的互化,考查三角函数的性质,考查计算能力,是一道中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 满意级别 | 非常满意 | 满意 | 一般 | 不满意 |
| 满意指数(分) | 90 | 60 | 30 | 0 |
| 人数(个) | 14 | 10 | 5 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com