
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
. |
| C |
. |
| B |
. |
| A |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
. |
| C |
. |
| B |
. |
| A |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| C | 0 3 |
| 1 |
| 3 |
| 1 |
| 27 |
| C | 1 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 9 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
| C | 3 3 |
| 2 |
| 3 |
| 8 |
| 27 |
| X | 0 | 100 | 200 | 300 | ||||||||
| P |
|
|
|
|
| 1 |
| 27 |
| 2 |
| 9 |
| 4 |
| 9 |
| 8 |
| 27 |
| 2 |
| 3 |
| 2 |
| 3 |


科目:高中数学 来源: 题型:
| 1 |
| 4 |
2
| ||
| 5 |
| MA |
| AF |
| MB |
| BF |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 销售经验(年) | 1 | 3 | 4 | 6 | 10 | 12 |
| 年销售额(万元) | 8 | 9.5 | 9 | 10.5 | 11 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 在三棱锥S-ABC中,O是AB的中点,SA=SB=
在三棱锥S-ABC中,O是AB的中点,SA=SB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| |||||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
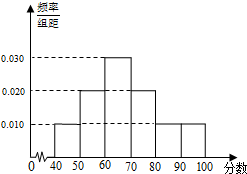 某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生的成绩进行统计,得到如图所示的样本频率分布直方图.若规定60分及以上为合格,则估计这1000名学生中合格人数是
某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生的成绩进行统计,得到如图所示的样本频率分布直方图.若规定60分及以上为合格,则估计这1000名学生中合格人数是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com