练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    由抛物线y2=x和直线x=1所围成图形的面积为    ．
    【答案】分析：先计算抛物线y2=x和直线x=1的交点纵坐标，确定积分上下限，再由定积分的几何意义，将图形面积问题转化为上下两函数差的定积分问题，最后利用微积分基本定理求值即可
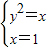
    解答：解：由得y=±1
    由定积分的几何意义知：
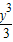
    由抛物线y2=x和直线x=1所围成图形的面积S=∫-11（1-y2）dy=（y-）|-11=（1-）-（-1+）=
    故答案为
    点评：本题考查了定积分的几何意义和微积分基本定理，解题时要注意恰当选择积分变量，简化运算过程．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    由抛物线y2=x和直线x=1所围成图形的面积为
    4
    3
    4
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源：中山市东升高中2008届高三数学基础达标训练6 题型：022

    (理)由抛物线y2＝x和直线x＝1所围成图形的面积为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    由抛物线y2=x和直线x=1所围成图形的面积为________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    由抛物线y2=x和直线x=1所围成图形的面积为______．

    查看答案和解析>>

    同步练习册答案