练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f(x)=为奇函数,则实数a=　　　　.

     

    -1

    【解析】显然f(x)的定义域为R,由题意,得f(0)==0,∴a=-1.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学文二轮专题复习与测试选修4-5不等式选讲 练习卷（解析版） 题型：解答题

    已知函数f(x)＝|2x－1|＋|2x＋a|，g(x)＝x＋3.

    (1)当a＝－2时，求不等式f(x)<g(x)的解集；

    (2)设a>－1时，且当x∈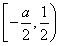时，f(x)≤g(x)，求a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学文二轮专题复习与测试解答题保分训练练习卷（解析版） 题型：解答题

    已知m＝(2cos x＋2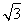sin x,1)，n＝(cos x，－y)，且m⊥n.

    (1)将y表示为x的函数f(x)，并求f(x)的单调递增区间；

    (2)已知a，b，c分别为△ABC的三个内角A，B，C对应的边长，若f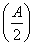＝3，且a＝2，b＋c＝4，求△ABC的面积．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（四）第二章第一节练习卷（解析版） 题型：选择题

    已知g(x)=1-2x,f(g(x))=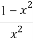(x≠0),那么f()等于(　　)

    (A)15 (B)1 (C)3 (D)30

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（六）第二章第三节练习卷（解析版） 题型：解答题

    已知函数f(x)=2|x-2|+ax(x∈R)有最小值.

    (1)求实数a的取值范围.

    (2)设g(x)为定义在R上的奇函数,且当x<0时,g(x)=f(x),求g(x)的解析式.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（六）第二章第三节练习卷（解析版） 题型：选择题

    对于函数f(x)=acosx+bx2+c,其中a,b,c∈R,适当地选取a,b,c的一组值计算f(1)和f(-1),所得出的正确结果只可能是(　　)

    (A)4和6 (B)3和-3

    (C)2和4 (D)1和1

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（八）第二章第五节练习卷（解析版） 题型：解答题

    已知函数f(x)=-x+log2.

    (1)求f()+f(-)的值.

    (2)当x∈(-a,a],其中a∈(0,1),a是常数时,函数f(x)是否存在最小值?若存在,求出f(x)的最小值;若不存在,请说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（五）第二章第二节练习卷（解析版） 题型：填空题

    函数f(x)=x2-kx+1在[1,2]上单调,则k的取值范围为　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（九）第二章第六节练习卷（解析版） 题型：选择题

    实数a=0.,b=log30.3,c=的大小关系正确的是(　　)

    (A)a<c<b (B)a<b<c

    (C)b<a<c (D)b<c<a

     

    查看答案和解析>>

    同步练习册答案