
已知数列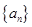 中,
中,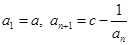 .
.
(Ⅰ)设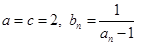 ,求数列
,求数列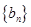 的通项公式;
的通项公式;
(Ⅱ)设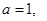 求证:
求证: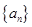 是递增数列的充分必要条件是
是递增数列的充分必要条件是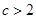 .
.
(Ⅰ)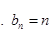 ;
;
(Ⅱ)证明:“必要性”数列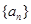 递增
递增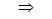

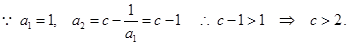
“充分性”用“数学归纳法”证明。
【解析】
试题分析:(Ⅰ)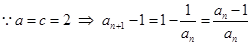
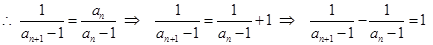
 是公差为
是公差为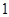 的等差数列,
的等差数列,
又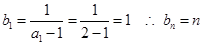 6分
6分
(Ⅱ)证明:“必要性”
数列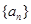 递增
递增

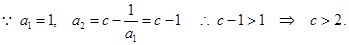 9分
9分
“充分性”
以下用“数学归纳法”证明,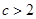 时,
时,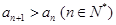 成立
成立
①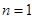 时,
时,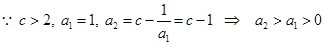 成立;
成立;
②假设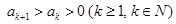 成立, 则
成立, 则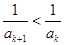
那么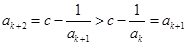
即 时,
时,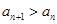 成立
成立
综合①②得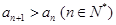 成立。
成立。
即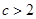 时,
时, 递增, 故,充分性得证。 13分
递增, 故,充分性得证。 13分
考点:本题主要考查等差数列的定义,充要条件证明问题,数学归纳法。
点评:确定数列的特征,一般要利用“定义法”或通过确定数列的通项公式,使问题得解。证明充要性问题,要证明“充分性”“必要性”两个方面,顺序上可根据难易调整。利用数学归纳法证明不等式,要注意遵循“两步一结”。


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
| 2n-1 |
| an•an+1 |
| 1 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com