【题目】在数列{an}中，a1＝1，an＋1＝2an＋2n.
(1)设bn＝
.证明：数列{bn}是等差数列；
(2)求数列{an}的前n项和．
【答案】（1）见解析（2）Sn＝(n－1)·2n＋1.
【解析】试题分析：（1）由
及条件可得
，即
，可得数列
为等差数列；
（2）由（1）得
，从而可得
，利用错位相减法求和即可。
试题解析：
(1)证明：∵ an＋1＝2an＋2n，
∴ bn＋1＝
＝
＝
＋1＝bn＋1.
∴bn＋1－bn＝1，
又b1＝a1＝1.
∴数列{bn}是首项为1，公差为1的等差数列．
(2)解：由(1)知，bn＝n，
∴＝bn＝n.
∴an＝n·2n－1.
∴Sn＝1＋2·21＋3·22＋…＋n·2n－1，①
∴2Sn＝1×21＋2·22＋…＋(n－1)·2n－1＋n·2n，②
①-②得：
－Sn＝1＋21＋22＋…＋2n－1－n·2n
∴Sn＝(n－1)2n＋1.
单元期中期末卷系列答案科目：高中数学 来源： 题型：
【题目】设函数f（x）= 
sin 
，若存在f（x）的极值点x0满足x02+[f（x0）]2＜m2 ， 则m的取值范围是（ ）
A.（﹣∞，﹣6）∪（6，+∞）
B.（﹣∞，﹣4）∪（4，+∞）
C.（﹣∞，﹣2）∪（2，+∞）
D.（﹣∞，﹣1）∪（1，+∞）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学初一年级500名学生参加某次数学测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20,30），[30,40），…，[80,90]，并整理得到如下频率分布直方图：
（1）从总体的500名学生中随机抽取一人，估计其分数小于70的概率；
（2）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】写出由下列各组命题构成的“p或q”“p且q”以及“非p”形式的命题，并判断它们的真假：
(1)p：3是素数，q：3是偶数；
(2)p：x＝－2是方程x2＋x－2＝0的解，q：x＝1是方程x2＋x－2＝0的解．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ax+ 
的图象经过点A（1，1），B（2，﹣1）．
（1）求函数f（x）的解析式；
（2）判断函数f（x）在（0，+∞）上的单调性并用定义证明；
（3）求f（x）在区间[ 
，1]上的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
．
（1）判断函数f（x）的奇偶性；
（2）判断并证明f（x）的单调性；
（3）求关于x的不等式f（2x﹣1）+f（x+3）＞0的解集．
查看答案和解析>>
科目：高中数学 来源： 题型：
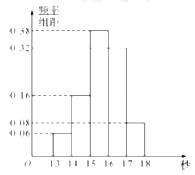
【题目】某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果按如下方式分成五组：第一组
，第二组
，…，第五组
，如图是按上述分组方法得到的频率分布直方图.
（Ⅰ）根据频率分布直方图，估计这50名学生百米测试成绩的中位数和平均数（精确到0.1）.
（Ⅱ）若从第一、五组中随机取出三名学生成绩，设取自第一组的个数为
，求
的分布列，期望及方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
