
【题目】已知曲线![]() 上的点到点
上的点到点![]() 的距离比到直线
的距离比到直线![]() 的距离小
的距离小![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)过点![]() 且倾斜角为
且倾斜角为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积;
的面积;
(2)设![]() 为曲线
为曲线![]() 上任意一点,点
上任意一点,点![]() ,是否存在垂直于
,是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在,求出
为直径的圆截得的弦长恒为定值?若存在,求出![]() 的方程和定值;若不存在,说明理由.
的方程和定值;若不存在,说明理由.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 存在,其方程为
存在,其方程为![]() ,定值为
,定值为![]() .
.
【解析】
(1)利用抛物线的定义可求得曲线![]() 的方程,由题意可得直线
的方程,由题意可得直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立,列出韦达定理,利用三角形的面积公式可求得
的方程联立,列出韦达定理,利用三角形的面积公式可求得![]() 的面积;
的面积;
(2)假设满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,并设点
,并设点![]() ,求出以
,求出以![]() 为直径的圆的方程,将
为直径的圆的方程,将![]() 代入圆的方程,求出弦长的表达式,进而可求得
代入圆的方程,求出弦长的表达式,进而可求得![]() 的值,由此可求得直线
的值,由此可求得直线![]() 的方程.
的方程.
(1)依题意得,曲线![]() 上的点到点
上的点到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等,
的距离相等,
所以曲线![]() 的方程为:
的方程为:![]() .
.
过点![]() 且倾斜角为
且倾斜角为![]() 的直线方程为
的直线方程为![]() ,
,
设![]() ,
,![]() ,联立
,联立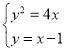 ,得
,得![]() ,
,
则![]() ,
,![]() ,则
,则![]() ;
;
(2)假设满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,设点
,设点![]() ,
,
则以![]() 为直径的圆的方程为
为直径的圆的方程为![]() ,
,
将直线![]() 代入,得
代入,得![]() ,
,
则![]() ,
,
设直线![]() 与以
与以![]() 为直径的圆的交点为
为直径的圆的交点为![]() 、
、![]() ,
,
则![]() ,
,![]() ,
,
于是有![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 为定值.
为定值.
故满足条件的直线![]() 存在,其方程为
存在,其方程为![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱![]() 中,侧棱与底面垂直,且
中,侧棱与底面垂直,且![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
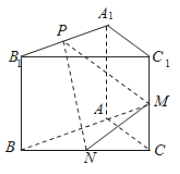
(1)求证:不论![]() 取何值,总有
取何值,总有![]() ;
;
(2)当![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知6名某疾病病毒密切接触者中有1名感染病毒,其余5名健康,需要通过化验血液来确定感染者.血液化验结果呈阳性的即为感染者,呈阴性即为健康.
(1)若从这6名密切接触者中随机抽取3名,求抽到感染者的概率;
(2)血液化验确定感染者的方法有:①逐一化验;②分组混合化验:先将血液分成若干组,对组内血液混合化验,若化验结果呈阴性,则该组血液不含病毒;若化验结果呈阳性,则对该组的备份血液逐一化验,直至确定感染者.
(i)采取逐一化验,求所需检验次数![]() 的数学期望;
的数学期望;
(ii)采取平均分组混合化验(每组血液份数相同),依据所需化验总次数的期望,选择合理的平均分组方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的内角A,B,C所对的边分别是a,b,c,其面积S
的内角A,B,C所对的边分别是a,b,c,其面积S![]() .
.
(1)若a![]() ,b
,b![]() ,求cosB.
,求cosB.
(2)求sin(A+B)+sinBcosB+cos(B﹣A)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为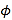 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,点
的交点,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,
的交点,![]() 、
、![]() 均异于原点
均异于原点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅱ)若![]() ,
,![]() ,求实数
,求实数![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,给出一个新数列
时,给出一个新数列![]() ,其中
,其中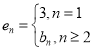 ,设这个新数列的前
,设这个新数列的前![]() 项和为
项和为![]() ,若
,若![]() 可以写成
可以写成![]() (
(![]() ,
,![]() 且
且![]() ,
,![]() )的形式,则称
)的形式,则称![]() 为“指数型和”.问
为“指数型和”.问![]() 中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC–A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点.过B1C1和P的平面交AB于E,交AC于F.
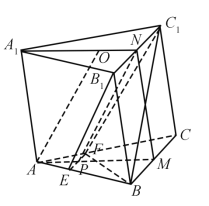
(1)证明:AA1//MN,且平面A1AMN⊥平面EB1C1F;
(2)设O为△A1B1C1的中心,若AO=AB=6,AO//平面EB1C1F,且∠MPN=![]() ,求四棱锥B–EB1C1F的体积.
,求四棱锥B–EB1C1F的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com