
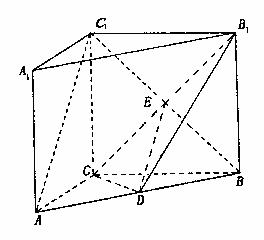
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求证:AC 1//平面CDB1;
(Ⅲ)求异面直线AC1与B1C所成角的余弦值.
(16)
解法一:

(Ⅰ)∵直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
∴ AC⊥BC,且BC1在平面ABC内的射影为BC,
∴ AC⊥BC1;
(Ⅱ)设CB1与C1B的交点为E,连结DE,
∵ D是AB的中点,E是BC1的中点,
∴ DE//AC1.
∵ DE![]() 平面CDB1,AC1
平面CDB1,AC1![]() 平面CDB1,
平面CDB1,
∴ AC1//平面CDB1;
(Ⅲ)∵ DE//AC1,∴∠CED为AC1与B1C所成的角,
在△CED中,ED=![]() AC 1=
AC 1=![]() ,CD=
,CD=![]() AB=
AB=![]() ,CE=
,CE=![]() CB1=2
CB1=2![]() ,
,
∴cos ,
,
∴ 异面直线AC1与B1C所成角的余弦值为![]() .
.
解法二:
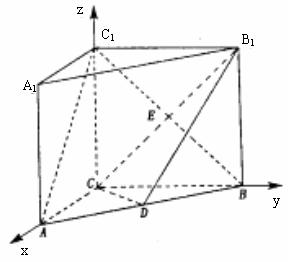
∵直三棱柱ABC-A1B1C1底面三边长AC=3,BC=4,AB=5,
∴AC,BC,C1C两两垂直。
如图,以C为坐标原点,直线CA,CB,CC1分别为x轴,y轴,z轴,建立空间直角坐标系,
则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4),
D(![]() ,2,0).
,2,0).
(Ⅰ)∵![]() =(-3,0,0),
=(-3,0,0),![]() =(0,-4,4),
=(0,-4,4),
∴![]() ·
·![]() =0,∴AC⊥BC1.
=0,∴AC⊥BC1.
(Ⅱ)设CB1与C1B的交点为E,则E(0,2,2).
∵![]() =(-
=(-![]() ,0,2),
,0,2),![]() =(-3,0,4),∴
=(-3,0,4),∴![]() =
=![]()
![]() ,∴DE//AC1.
,∴DE//AC1.
∵DE![]() 平面CDB1,AC1
平面CDB1,AC1![]() 平面CDB1,∴AC1//平面CDB1.
平面CDB1,∴AC1//平面CDB1.
(Ⅲ)∵![]() =(-3,0,4),
=(-3,0,4),![]() =(0,4,4),
=(0,4,4),
∴cos<![]() ,
,![]() >=
>=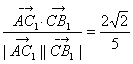 ,
,
∴异面直线AC1与B![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
 如图,在平行四边形ABCD中,2|AB|2+|BD|2-4=0,∠ABD=90°,沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的表面积是( )
如图,在平行四边形ABCD中,2|AB|2+|BD|2-4=0,∠ABD=90°,沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的表面积是( )查看答案和解析>>
科目:高中数学 来源: 题型:
(I)求证:BD⊥A1C;
(II)求二面角A 1-BD-C 1的大小;
(III)求异面直线 AD与 BC 1所成角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
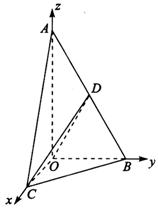
(Ⅰ)求证:平面COD⊥平面AOB;
(Ⅱ)当D为AB的中点时,求异面直线AO与CD所成角的大小;
(Ⅲ)求CD与平面AOB所成角的最大值.
查看答案和解析>>
科目:高中数学 来源:2012年陕西省西安市西工大附中高考数学八模试卷(理科)(解析版) 题型:选择题
 如图,在平行四边形ABCD中,2|AB|2+|BD|2-4=0,∠ABD=90°,沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的表面积是( )
如图,在平行四边形ABCD中,2|AB|2+|BD|2-4=0,∠ABD=90°,沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的表面积是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com