
【题目】已知: ![]() =(2sinx,2cosx),
=(2sinx,2cosx), ![]() =(cosx,﹣cosx),f(x)=
=(cosx,﹣cosx),f(x)= ![]() .
.
(1)若 ![]() 与
与 ![]() 共线,且x∈(
共线,且x∈( ![]() ,π),求x的值;
,π),求x的值;
(2)求函数f(x)的周期;
(3)若对任意x∈[0, ![]() ]不等式m﹣2≤f(x)≤m+
]不等式m﹣2≤f(x)≤m+ ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】
(1)解:∵x∈( ![]() ,π),∴cosx≠0
,π),∴cosx≠0
又∵ ![]() 与
与 ![]() 共线∴
共线∴ ![]() =
= ![]() 即tanx=﹣1
即tanx=﹣1
∵x∈( ![]() ,π),∴x=
,π),∴x= ![]() =
= ![]()
(2)解:f(x)= ![]() =2sinxcosx﹣2cos2x=sin2x﹣cos2x﹣1
=2sinxcosx﹣2cos2x=sin2x﹣cos2x﹣1
= ![]() (sin2x
(sin2x ![]() ﹣cos2x
﹣cos2x ![]() )=
)= ![]() sin(2x﹣
sin(2x﹣ ![]() )﹣1
)﹣1
故函数f(x)的周期T= ![]() =π
=π
(3)解:∵0 ![]()
∴ ![]() ≤
≤ ![]()
∴ ![]() ≤sin(2x﹣
≤sin(2x﹣ ![]() )≤1
)≤1
∴﹣2 ![]() ﹣1
﹣1 ![]() ,
,
即﹣2 ![]()
要使不等式m﹣2≤f(x) ![]() ,
,
对任意x ![]() ]上恒成立,
]上恒成立,
必须且只需 ![]() ,
,
即﹣1≤m≤0.
【解析】(1)运用共线的向量的性质得出 ![]() =
= ![]() 即tanx=﹣1,结合x∈(
即tanx=﹣1,结合x∈( ![]() ,π),求解x的值.(2)化简得出f(x)=
,π),求解x的值.(2)化简得出f(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() )﹣1,根据三角函数的性质得出周期,T═
)﹣1,根据三角函数的性质得出周期,T═ ![]() (3)根据x的范围得出
(3)根据x的范围得出 ![]() ≤sin(2x﹣
≤sin(2x﹣ ![]() )≤1,确定﹣2
)≤1,确定﹣2 ![]() ,利用最大值,最小值问题求解得出只需
,利用最大值,最小值问题求解得出只需 ![]() 成立即可.
成立即可.


科目:高中数学 来源: 题型:
【题目】对于给定的正整数k,若数列{an}满足![]()
=2kan对任意正整数n(n> k) 总成立,则称数列{an} 是“P(k)数列”.
(1)证明:等差数列{an}是“P(3)数列”;
若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,网格纸上小正方形的边长为![]() ,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
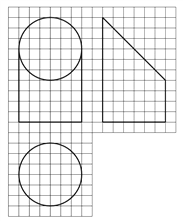
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() 为正三角形,平面
为正三角形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定点
?若存在,请确定点![]() 的位置并证明;若不存在,说明理由.
的位置并证明;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com