【题目】在直角坐标系
中，曲线
的参数方程为
，（
为参数），以坐标原点为极点，
轴的正半轴为极轴，建立极坐标系，曲线
的极坐标方程为
.
（1）写出曲线的极坐标方程和曲线的直角坐标方程；
（2）若射线
与曲线相交于点
，将
逆时针旋转
后，与曲线相交于点
，且
，求
的值.
教材全解字词句篇系列答案科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，四边形ABCD为正方形，
平面ACD，且
，E为PD的中点．
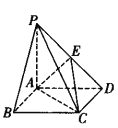
（Ⅰ）证明：平面
平面PAD；
（Ⅱ）求直线PA与平面AEC所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂生产某种型号的电视机零配件，为了预测今年
月份该型号电视机零配件的市场需求量，以合理安排生产，工厂对本年度
月份至
月份该型号电视机零配件的销售量及销售单价进行了调查，销售单价
（单位：元）和销售量
（单位：千件）之间的组数据如下表所示：
月份 |
|
|
|
|
|
|
销售单价 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
（1）根据1至月份的数据，求关于的线性回归方程（系数精确到
）；
（2）结合（1）中的线性回归方程，假设该型号电视机零配件的生产成本为每件
元，那么工厂如何制定月份的销售单价，才能使该月利润达到最大（计算结果精确到
）？
参考公式：回归直线方程
，其中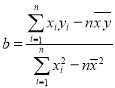
.
参考数据：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】每个国家对退休年龄都有不一样的规定，从2018年开始，我国关于延迟退休的话题一直在网上热议，为了了解市民对“延迟退休”的态度，现从某地市民中随机选取100人进行调查，调查情况如下表：
年龄段（单位：岁） |
|
|
|
|
|
|
被调查的人数 |
|
|
|
|
|
|
赞成的人数 |
|
|
|
|
|
|
（1）从赞成“延迟退休”的人中任选1人，此人年龄在
的概率为
，求出表格中
的值；
（2）若从年龄在
的参与调查的市民中按照是否赞成“延迟退休”进行分层抽样，从中抽取10人参与某项调查，然后再从这10人中随机抽取4人参加座谈会，记这4人中赞成“延迟退休”的人数为
，求的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，椭圆
，
、
，为椭圆
的左、右顶点．
设
为椭圆的左焦点，证明:当且仅当椭圆上的点
在椭圆的左、右顶点时，
取得最小值与最大值．
若椭圆上的点到焦点距离的最大值为
，最小值为
，求椭圆的标准方程．
若直线
与中所述椭圆相交于
、
两点（、不是左、右顶点），且满足
，求证：直线
过定点，并求出该定点的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设X～N(μ1，
)，Y～N(μ2，
)，这两个正态分布密度曲线如图所示，下列结论中正确的是 ( )
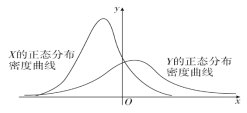
A. P(Y≥μ2)≥P(Y≥μ1)
B. P(X≤σ2)≤P(X≤σ1)
C. 对任意正数t，P(X≥t)≥P(Y≥t)
D. 对任意正数t，P(X≤t)≥P(Y≤t)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
