
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)函数![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数a的值;
垂直,求实数a的值;
(2)若函数![]() 在定义域上有两个极值点
在定义域上有两个极值点![]() ,
,![]() ,且
,且![]() .
.
①求实数a的取值范围;
②求证:![]() .
.
【答案】(1)2;(2)①![]() ;②见解析.
;②见解析.
【解析】
(1)利用导数的几何意义列式![]() 求解;(2)①由题意可知
求解;(2)①由题意可知![]() 在
在![]() 上有两个根
上有两个根![]() ,
,![]() ,且
,且![]() ,即
,即![]() 在
在![]() 上有两个不相等的根
上有两个不相等的根![]() ,
,![]() ,列式求实数
,列式求实数![]() 的范围;②由①可知
的范围;②由①可知 其中
其中![]() ,
,![]() ,整理代入根与系数的关系,
,整理代入根与系数的关系,![]() ,转化为证明
,转化为证明![]() 恒成立.
恒成立.
(1)依题意,![]() ,故
,故![]() ,所以
,所以![]()
据题意可知,![]() ,解得
,解得![]() .所以实数a的值为2.
.所以实数a的值为2.
(2)①因为函数![]() 在定义域上有两个极值点
在定义域上有两个极值点![]() ,
,![]() ,且
,且![]() ,
,
所以![]() 在
在![]() 上有两个根
上有两个根![]() ,
,![]() ,且
,且![]() ,
,
即![]() 在
在![]() 上有两个不相等的根
上有两个不相等的根![]() ,
,![]()
所以 ,解得
,解得![]() ,当
,当![]() 时,若
时,若![]() 或
或![]() ,
,
![]() ,
,![]() ,函数
,函数![]() 在
在![]() 和
和![]() 上单调递增;
上单调递增;
若![]() ,
,![]() ,
,![]() ,函数
,函数![]() 在
在![]() 上单调递减,
上单调递减,
故函数![]() 在
在![]() 上有两个极值点
上有两个极值点![]() ,
,![]() ,且
,且![]() .所以,实数a的取值范围是
.所以,实数a的取值范围是![]() .
.
②由①可知,![]() 是方程
是方程![]() 的两个不等的实根,
的两个不等的实根,
所以 其中
其中![]() .
.
故![]()
![]()
![]()
![]() ,
,
令![]() ,其中
,其中![]() .故
.故![]() ,
,
令![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
由于![]() ,
,![]() ,所以存在常数
,所以存在常数![]() ,使得
,使得![]() ,
,
即![]() ,
,![]() .且当
.且当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,![]()
又![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() .
.
故![]() 得证.
得证.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,已知椭圆 C:![]() 的离心率为
的离心率为![]() ,且过点 (
,且过点 (![]() ,
,![]() ),点 P 在第四象限, A 为左顶点, B 为上顶点, PA 交 y 轴于点 C,PB 交 x 轴于点 D.
),点 P 在第四象限, A 为左顶点, B 为上顶点, PA 交 y 轴于点 C,PB 交 x 轴于点 D.

(1) 求椭圆 C 的标准方程;
(2) 求 △PCD 面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有学生500人,学校为了解学生的课外阅读时间,从中随机抽取了50名学生,获得了他们某一个月课外阅读时间的数据(单位:小时),将数据分为5组:[10,12),[12,14),[14,16),[16,18),[18,20],整理得到如图所示的频率分布直方图.
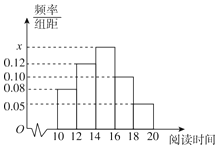
(1)求频率分布直方图中的x的值;
(2)试估计该校所有学生中,课外阅读时间不小于16小时的学生人数;
(3)已知课外阅读时间在[10,12)的样本学生中有3名女生,现从阅读时间在[10,12)的样本学生中随机抽取3人,记X为抽到女生的人数,求X的分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某种螺帽是由一个半径为2的半球体挖去一个正三棱锥构成的几何体,该正三棱锥的底面三角形内接于半球底面大圆,顶点在半球面上,则被挖去的正三棱锥体积为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a,b
(a,b![]() R).
R).
(1)当a=b=1时,求![]() 的单调增区间;
的单调增区间;
(2)当a≠0时,若函数![]() 恰有两个不同的零点,求
恰有两个不同的零点,求![]() 的值;
的值;
(3)当a=0时,若![]() 的解集为(m,n),且(m,n)中有且仅有一个整数,求实数b的取值范围.
的解集为(m,n),且(m,n)中有且仅有一个整数,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC—A1B1C1中,四边形AA1B1B为矩形,平面AA1B1B⊥平面ABC,点E,F分别是侧面AA1B1B,BB1C1C对角线的交点.
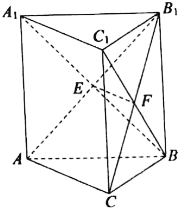
(1)求证:EF∥平面ABC;
(2)BB1⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把![]() ,
,![]() ,
,![]() ,
,![]() 四本不同的书分给三位同学,每人至少分到一本,每本书都必须有人分到,
四本不同的书分给三位同学,每人至少分到一本,每本书都必须有人分到,![]() ,
,![]() 不能同时分给同一个人,则不同的分配方式共有__________种(用数字作答).
不能同时分给同一个人,则不同的分配方式共有__________种(用数字作答).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com