
分析 (1)求出圆心与半径,即可求圆C的方程;
(2)利用代入法,求线段PQ中点M的轨迹方程.
解答 解:(1)圆心坐标为C(3,2),又半径r=|OC|=$\sqrt{13}$,
则所求圆的方程是(x-3)2+(y-2)2=13.
(2)设线段PQ的中点M(x,y),P(x0,y0)
M为线段PQ的中点,则x0=2x-8,y0=2y.
P(2x-8,2y)代入圆C中得(2x-8-3)2+(2y-2)2=13,
即线段PQ中点M的轨迹方程为(x-$\frac{11}{2}$)2+(y-1)2=$\frac{13}{4}$.
点评 本题考查圆的方程,考查代入法的运用,确定坐标之间的关系是关键.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
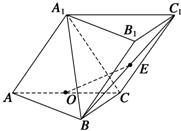 三棱柱ABC-A1B1C1中,A1-AC-B是直二面角,AA1=A1C=AC=2,AB=BC且∠ABC=90°,O为AC的中点.
三棱柱ABC-A1B1C1中,A1-AC-B是直二面角,AA1=A1C=AC=2,AB=BC且∠ABC=90°,O为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $-\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
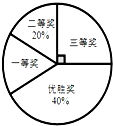 国务院办公厅在去年3月发布了《中国足球发展改革总体方案》,为进一步普及足球知识,传播足球文化,我市某县在中小学举行“足球在身边”知识竞赛活动,各类获奖学生人数比例如图的示,其中获得三等奖共50名学生,结合图中信息,解答下列问题:
国务院办公厅在去年3月发布了《中国足球发展改革总体方案》,为进一步普及足球知识,传播足球文化,我市某县在中小学举行“足球在身边”知识竞赛活动,各类获奖学生人数比例如图的示,其中获得三等奖共50名学生,结合图中信息,解答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{19}$ | B. | $\sqrt{13}$ | C. | $\sqrt{10}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com