
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $-\sqrt{3}$ |
分析 由等差数列和等比数列的性质求出b3+b9,1-a4a8的值,代入$tan\frac{{{b_3}+{b_9}}}{{1-{a_4}•{a_8}}}$得答案.
解答 解:在等差数列{bn}中,由b1+b6+b11=7π,得3b6=7π,${b}_{6}=\frac{7π}{3}$,
∴${b}_{3}+{b}_{9}=2{b}_{6}=\frac{14π}{3}$,
在等比数列{an}中,由${a}_{1}{a}_{6}{a}_{11}=-3\sqrt{3}$,得${{a}_{6}}^{3}=-3\sqrt{3}$,${a}_{6}=-\sqrt{3}$,
∴$1-{a}_{4}{a}_{8}=1-(-\sqrt{3})^{2}=-2$,
则$tan\frac{{{b_3}+{b_9}}}{{1-{a_4}•{a_8}}}$=tan$\frac{\frac{14π}{3}}{-2}$=tan$(-\frac{7π}{3})$=$-\sqrt{3}$.
故选:D.
点评 本题考查等差数列与等比数列的综合题,考查等差数列与等比数列的性质,训练了三角函数值的求法,是中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=sin(x-\frac{π}{4})$ | B. | $y=cos(x+\frac{π}{4})$ | C. | $y=sin(2x+\frac{π}{4})$ | D. | $y=cos(2x-\frac{π}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
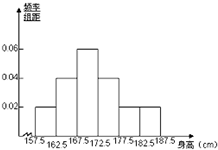 某省2015年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5),第二组[162.5,167.5),…,第6组[182.5,187.5),图是按上述分组方法得到的频率分布直方图.
某省2015年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5),第二组[162.5,167.5),…,第6组[182.5,187.5),图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com