
分析 将行列式按第一列展开,求得不等式lg2x-2lgx≤0,设lgx=t,t∈R,求得t的取值范围,代入即可求得x的解集.
解答 解:$|\begin{array}{l}{l{g}^{2}x}&{2}&{4}\\{2lgx}&{1}&{1}\\{0}&{1}&{3}\end{array}|$=lg2x×$|\begin{array}{l}{1}&{1}\\{1}&{3}\end{array}|$-2lgx$|\begin{array}{l}{2}&{4}\\{1}&{3}\end{array}|$=2(lg2x-2lgx),
∴lg2x-2lgx≤0,
设lgx=t,t∈R,
∴t2-2t≤0,解得:0≤t≤2,
∴0≤lgx≤2,
解得:1≤x≤100,
故答案为:{x丨1≤x≤100}.
点评 本题考查行列式的展开,考查一元二次不等式的解集,考查计算能力,属于中档题.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -3 | C. | 3 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
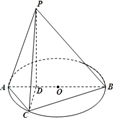 如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=$\frac{1}{3}$DB,点C为圆O上一点,且BC=$\sqrt{3}$AC.点P在圆O所在平面上的正投影为点D,PD=BD.
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=$\frac{1}{3}$DB,点C为圆O上一点,且BC=$\sqrt{3}$AC.点P在圆O所在平面上的正投影为点D,PD=BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{2}+1$ | C. | $\sqrt{2}-1$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | arctan(-6) | B. | arctan(-$\frac{1}{6}$) | C. | π-arctan6 | D. | π-arctan$\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com