
分析 (1)将行列式按第二行展开求得Sn的表达式,当n=1时,求得a1,当n≥2时,Sn-1=$\frac{π}{6}$(n-1)2+$\frac{π}{12}$(n-1),即可求得通项公式an;
(2)由(1)可知,将Sn代入,求得bn,根据行列式展开,求得cn的通项公式,利用“裂项法”即可求得数列{cn}的前n项和Tn,求得$\frac{{T}_{n}}{n}$,即可求得$\underset{lim}{n→∞}$$\frac{{T}_{n}}{n}$.
解答 解:(1)Sn=n×$|\begin{array}{l}{\frac{π}{6}}&{\frac{π}{12}}\\{-1}&{n}\end{array}|$=$\frac{π}{6}$n2+$\frac{π}{12}$n,
Sn=$\frac{π}{6}$n2+$\frac{π}{12}$n,
当n=1时,a1=$\frac{π}{4}$,
当n≥2时,Sn-1=$\frac{π}{6}$(n-1)2+$\frac{π}{12}$(n-1),
两式相减得:an=$\frac{π}{3}$n-$\frac{π}{12}$,
当n=1,成立,
∴数列{an}通项公式an=$\frac{π}{3}$n-$\frac{π}{12}$;
(2)bn=$\frac{πn}{12{S}_{n}}$=$\frac{πn}{12×\frac{π}{12}n(2n+1)}$=$\frac{1}{2n+1}$,
cn=$|\begin{array}{l}{{b}_{n}}&{1}\\{1}&{{b}_{n+1}}\end{array}|$=bn•bn+1-1=$\frac{1}{(2n+1)(2n+3)}$-1=$\frac{1}{2}$($\frac{1}{2n+1}$-$\frac{1}{2n+3}$)-1,
Tn=c1+c2+c3+…+cn=$\frac{1}{2}$[($\frac{1}{3}$-$\frac{1}{5}$)+($\frac{1}{5}$-$\frac{1}{7}$)+…+($\frac{1}{2n+1}$-$\frac{1}{2n+3}$)]-n,
=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{2n+3}$)-n
=$\frac{-2n(3n+4)}{3(2n+3)}$,
∴Tn=$\frac{-2n(3n+4)}{3(2n+3)}$,
$\underset{lim}{n→∞}$$\frac{{T}_{n}}{n}$=$\underset{lim}{n→∞}$$\frac{-2(3n+4)}{3(2n+3)}$=-$\frac{2}{3}$$\underset{lim}{n→∞}$$\frac{3+\frac{4}{n}}{2+\frac{3}{n}}$=-$\frac{2}{3}$×$\frac{3}{2}$=-1,
∴$\underset{lim}{n→∞}$$\frac{{T}_{n}}{n}$=-1.
点评 本题考查三阶行列式展开,考查数列的通项公式,“裂项法”求前n项和公式、数列的极限,综合综合能力强,知识点多,考查分析问题及解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | k=2 | B. | k=2$\sqrt{2}$ | C. | k=$\sqrt{2}$ | D. | k=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
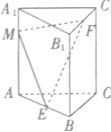 如图,已知ABC-A1B1C1是所有棱长均相等的正三棱柱,点E是棱AB的中点,点F是棱B1C1的中点,点M是棱AA1上的动点,则二面角B1-EM-F的正切值不可能等于( )
如图,已知ABC-A1B1C1是所有棱长均相等的正三棱柱,点E是棱AB的中点,点F是棱B1C1的中点,点M是棱AA1上的动点,则二面角B1-EM-F的正切值不可能等于( )| A. | $\frac{\sqrt{15}}{6}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{5}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com