
 =(1,1),
=(1,1), =(1,0),<
=(1,0),< ,
, >=
>= 且
且 =-1;若△ABC的内角A,B,C依次成等差数列,且A≤B≤C;
=-1;若△ABC的内角A,B,C依次成等差数列,且A≤B≤C; )=
)= 在[0,B]上有相异实根,求实数m的取值范围;
在[0,B]上有相异实根,求实数m的取值范围; =(cosA,2cos2
=(cosA,2cos2  ),试求|
),试求|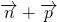 |的取值范围.
|的取值范围. . 令y=sin(2x+
. 令y=sin(2x+ ),x∈[0,
),x∈[0, ],则 2x+
],则 2x+ ∈[
∈[ ,π],∴
,π],∴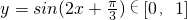 .
. )=
)= 在[0,
在[0, ]上有相异实根,所以y=sin(2x+
]上有相异实根,所以y=sin(2x+ )
)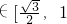 ),即
),即 ∈
∈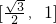
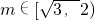 .
. =(x,y),∵
=(x,y),∵ =(1,1),
=(1,1), =-1,所以x+y=-1.
=-1,所以x+y=-1. =(1,0),<
=(1,0),< ,
, >=
>= ,所以
,所以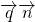 =0,即x=0,故y=-1,
=0,即x=0,故y=-1, =(0,-1),
=(0,-1), =(cosA,2cos2
=(cosA,2cos2  )=(cosA,1+cosC).
)=(cosA,1+cosC).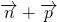 |2=cos2A+cos2C=cos2A+cos2(
|2=cos2A+cos2C=cos2A+cos2(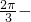 A)=1+
A)=1+ cos(2A+
cos(2A+ ).
).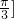 ,得2A+
,得2A+ ∈(
∈( ,π],得cos(2A+
,π],得cos(2A+ )∈[-1,
)∈[-1, ),
),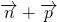 |2∈[
|2∈[ ,
, ),故|
),故|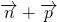 |∈[
|∈[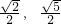 ).
). ,令y=sin(2x+
,令y=sin(2x+ ),由 x∈[0,
),由 x∈[0, ]求得y的值域,再由关于x的方程sin(2x+
]求得y的值域,再由关于x的方程sin(2x+ )=
)= 在[0,
在[0, ]上有相异实根,所以y=sin(2x+
]上有相异实根,所以y=sin(2x+ )
)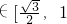 ),
), ∈
∈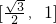 ,从而求得实数m的取值范围.
,从而求得实数m的取值范围. =(x,y),由条件
=(x,y),由条件 =-1可得x+y=-1.再由
=-1可得x+y=-1.再由 =(1,0),<
=(1,0),< ,
, >=
>= ,求得以
,求得以 和
和 的坐标,可得|
的坐标,可得|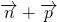 |2=1+
|2=1+ cos(2A+
cos(2A+ ),再由A的范围求出|
),再由A的范围求出|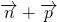 |的范围.
|的范围.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| m |
| n |
| m |
| 3π |
| 4 |
| m |
| n |
| n |
| a |
| b |
| π |
| 3 |
| x |
| 2 |
| a |
| n |
| m |
| n |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| 3 |
| 4 |
| a |
| b |
| b |
| b |
| q |
| π |
| 2 |
| p |
| C |
| 2 |
| 2 |
| 3 |
| b |
| p |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| π |
| 2 |
| 1 |
| 5 |
| sin2α-2sin2α |
| 1-tanα |
查看答案和解析>>
科目:高中数学 来源:设计选修数学2-1苏教版 苏教版 题型:013
已知向量a=(1,1,0),b=(-1,0,2)且ka+b与2a-b互相垂直,则k的值是
1
![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)已知向量a=(1,1),b=(1,0),c满足a·c=0且|a|=|c|,b·c>0.
(1)求向量c;(2)若映射f:(x,y)→(x1,y1)=xa+yc,求映射f下(1,2)的原象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com