
【题目】在平面直角坐标系中,已知曲线![]() :
: (
(![]() 为参数)和定点
为参数)和定点![]() ,
,![]() 是曲线
是曲线![]() 的左、右焦点,以原点
的左、右焦点,以原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴且取相同单位长度建立极坐标系.
轴的非负半轴为极轴且取相同单位长度建立极坐标系.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2)经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为![]() ,底面圆心为
,底面圆心为![]() ,半径为
,半径为![]() .
.
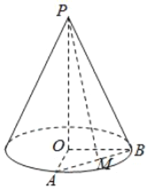
(1)设圆锥的母线长为![]() ,求圆锥的体积;
,求圆锥的体积;
(2)设![]() ,
,![]() 、
、![]() 是底面半径,且
是底面半径,且![]() ,
,![]() 为线段
为线段![]() 的中点,如图.求异面直线
的中点,如图.求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某山区小学有![]() 名四年级学生,将全体四年级学生随机按
名四年级学生,将全体四年级学生随机按![]() 编号,并且按编号顺序平均分成
编号,并且按编号顺序平均分成![]() 组.现要从中抽取
组.现要从中抽取![]() 名学生,各组内抽取的编号按依次增加
名学生,各组内抽取的编号按依次增加![]() 进行系统抽样.
进行系统抽样.
(1)若抽出的一个号码为![]() ,据此写出所有被抽出学生的号码;
,据此写出所有被抽出学生的号码;
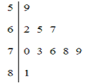
(2)分别统计这![]() 名学生的数学成绩,获得成绩数据的茎叶图如图所示,求该样本的方差.
名学生的数学成绩,获得成绩数据的茎叶图如图所示,求该样本的方差.
(注:![]() ,方差
,方差![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,点
,点![]() 分别为棱
分别为棱![]() 的中点,下列结论中,其中正确的个数是( )
的中点,下列结论中,其中正确的个数是( )
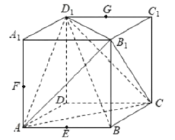
①过![]() 三点作正方体的截面,所得截面为正六边形;
三点作正方体的截面,所得截面为正六边形;
②![]() /平面
/平面![]() ;
;
③![]() ;
;
④异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ;
;
⑤四面体![]() 的体积等于
的体积等于![]()
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com