
【题目】已知某山区小学有![]() 名四年级学生,将全体四年级学生随机按
名四年级学生,将全体四年级学生随机按![]() 编号,并且按编号顺序平均分成
编号,并且按编号顺序平均分成![]() 组.现要从中抽取
组.现要从中抽取![]() 名学生,各组内抽取的编号按依次增加
名学生,各组内抽取的编号按依次增加![]() 进行系统抽样.
进行系统抽样.
(1)若抽出的一个号码为![]() ,据此写出所有被抽出学生的号码;
,据此写出所有被抽出学生的号码;
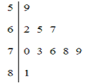
(2)分别统计这![]() 名学生的数学成绩,获得成绩数据的茎叶图如图所示,求该样本的方差.
名学生的数学成绩,获得成绩数据的茎叶图如图所示,求该样本的方差.
(注:![]() ,方差
,方差![]() )
)
 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系下,方程![]() 的图形为如图所示的“幸运四叶草”,又称为玫瑰线.
的图形为如图所示的“幸运四叶草”,又称为玫瑰线.

(1)当玫瑰线的![]() 时,求以极点为圆心的单位圆与玫瑰线的交点的极坐标;
时,求以极点为圆心的单位圆与玫瑰线的交点的极坐标;
(2)求曲线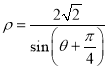 上的点M与玫瑰线上的点N距离的最小值及取得最小值时的点M、N的极坐标(不必写详细解题过程).
上的点M与玫瑰线上的点N距离的最小值及取得最小值时的点M、N的极坐标(不必写详细解题过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知二次函数![]() (
(![]() 、
、![]() 、
、![]() 均为实常数,
均为实常数,![]() )的最小值是0,函数
)的最小值是0,函数![]() 的零点是
的零点是![]() 和
和![]() ,函数
,函数![]() 满足
满足![]() ,其中
,其中![]() ,为常数.
,为常数.
(1)已知实数![]() 、
、![]() 满足、
满足、![]() ,且
,且![]() ,试比较
,试比较![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
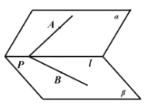
【题目】如图,二面角![]() 中,
中,![]() ,射线
,射线![]() ,
,![]() 分别在平面
分别在平面![]() ,
,![]() 内,点A在平面
内,点A在平面![]() 内的射影恰好是点B,设二面角
内的射影恰好是点B,设二面角![]() 、
、![]() 与平面
与平面![]() 所成角、
所成角、![]() 与平面
与平面![]() 所成角的大小分别为
所成角的大小分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() :
: (
(![]() 为参数)和定点
为参数)和定点![]() ,
,![]() 是曲线
是曲线![]() 的左、右焦点,以原点
的左、右焦点,以原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴且取相同单位长度建立极坐标系.
轴的非负半轴为极轴且取相同单位长度建立极坐标系.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2)经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长均相等的四棱锥![]() 中,
中, ![]() 为底面正方形的中心,
为底面正方形的中心, ![]() ,
,![]() 分别为侧棱
分别为侧棱![]() ,
,![]() 的中点,有下列结论正确的有:( )
的中点,有下列结论正确的有:( )

A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() ∥平面
∥平面![]()
C.直线![]() 与直线
与直线![]() 所成角的大小为
所成角的大小为![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() (
(![]() =1,2,…,6),如表所示:
=1,2,…,6),如表所示:
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 | q | 84 | 83 | 80 | 75 | 68 |
已知![]() .
.
(Ⅰ)求出![]() 的值;
的值;
(Ⅱ)已知变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(参考公式:线性回归方程中![]() ,
,![]() 的最小二乘估计分别为
的最小二乘估计分别为 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com