
分析 分别取n=1,2,3,得到关于a,b,c的方程组解得即可,先根据当n=1时,把n=1代入求值等式成立;再假设n=k时关系成立,利用变形可得n=k+1时关系也成立,综合得到对于任意n∈N*时都成立
解答 解:取n=1,2,3可得$\left\{\begin{array}{l}{a+b+c=1}\\{8a+4b+2c=5}\\{27a+9b+3c=14}\end{array}\right.$解得:a=$\frac{1}{3}$,b=$\frac{1}{2}$,c=$\frac{1}{6}$.
下面用数学归纳法证明($\frac{1}{n}$)2+($\frac{2}{n}$)2+($\frac{3}{n}$)2+…+($\frac{n}{n}$)2=$\frac{2{n}^{2}+3n+1}{6n}$=$\frac{(n+1)(2n+1)}{6n}$.
即证12+22+…+n2=$\frac{1}{6}$n(n+1)(2n+1),
①n=1时,左边=1,右边=1,∴等式成立;
②假设n=k时等式成立,即12+22+…+k2=$\frac{1}{6}$k(k+1)(2k+1)成立,
则当n=k+1时,等式左边=12+22+…+k2+(k+1)2═$\frac{1}{6}$k(k+1)(2k+1)+(k+1)2=$\frac{1}{6}$[k(k+1)(2k+1)+6(k+1)2]=$\frac{1}{6}$(k+1)(2k2+7k+6)=$\frac{1}{6}$(k+1)(k+2)(2k+3),
∴当n=k+1时等式成立;
由数学归纳法,综合①②当n∈N*等式成立,
故存在a=$\frac{1}{3}$,b=$\frac{1}{2}$,c=$\frac{1}{6}$使已知等式成立.
点评 本题主要考查归纳推理,数学归纳法,数列的通项等相关基础知识.考查运算化简能力、推理论证能力和化归思想


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-3<x<1} | B. | {x|-1<x<3}. | C. | {x|x<-3或x>1} | D. | {x|x<-1或x>3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
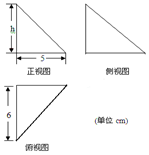 如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )
如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )| A. | 55π | B. | 75π | C. | 77π | D. | 65π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a=\sqrt{3}$ | B. | $a>\sqrt{3}$或$a<-\sqrt{3}$ | C. | $-\sqrt{3}<a<\sqrt{3}$ | D. | $-\sqrt{3}≤a≤\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
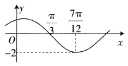 已知函数f(x)=Asin(wx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数的图象向左平移$\frac{π}{6}$个单位长度得到函数g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=Asin(wx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数的图象向左平移$\frac{π}{6}$个单位长度得到函数g(x)的图象,则函数g(x)的解析式为( )| A. | g(x)=2sin(2x-$\frac{π}{3}$) | B. | g(x)=2sin(2x+$\frac{π}{6}$) | C. | g(x)=-2sin(2x-$\frac{π}{3}$) | D. | g(x)=-2sin(2x+$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a-\overrightarrow b$ | B. | $\overrightarrow b-\overrightarrow a$ | C. | $\overrightarrow b+\overrightarrow a$ | D. | $-\overrightarrow a-\overrightarrow b$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com