
| A. | 减函数,且f(x)<0 | B. | 减函数,且f(x)>O | C. | 增函数,且f(x)<0 | D. | 增函数,且f(x)>0 |
分析 先设x∈(1,2),利用周期性和符号把“2-x”转化到区间(0,1),代入函数解析式,再利用奇函数的定义和周期性,求出f(x)在(1,2)上的解析式.
解答 解:设x∈(1,2),则-1<x-2<0,∴0<2-x<1,
∵当x∈(0,1)时,f(x)=log2x,∴f(2-x)=log2(2-x),
∵f(x)是R上以2为周期的奇函数,
∴f(x-2)=-f(2-x)=-log2(2-x),f(x)=f(x-2)=-log2(2-x),
∴f(x)=-log2(2-x),
由0<2-x<1,得:f(x)>0,是增函数,
故选:D.
点评 本题考查了求定区间上的函数解析式,一般的做法是“求谁设谁”,即在那个区间上求解析式,x就设在该区间内,再利用函数的周期和负号转化到已知的区间上,代入解析式进行化简,再利用奇函数的定义和周期性求出f(x).


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
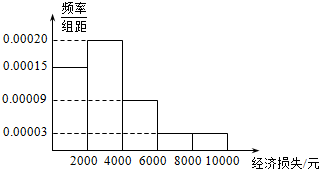 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图1):
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图1):| 经济损失不超过 4000元 | 经济损失超过 4000元 | 合计 | |
| 捐款超过 500元 | 30 | ||
| 捐款不超 过500元 | 6 | ||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
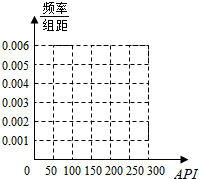 某城市随机抽取一年内100天的空气质量指数API的监测数据,结果统计如下:
某城市随机抽取一年内100天的空气质量指数API的监测数据,结果统计如下:| API | 空气质量 | 频数 | 频率 |
| [0,50] | 优 | 5 | 0.05 |
| [50,100] | 良 | ① | 0.2 |
| [100,150] | 轻度污染 | 25 | ② |
| [150,200] | 轻度污染 | 30 | 0.3 |
| [200,250] | 中度污染 | 10 | 0.1 |
| [250,300] | 中度重污染 | 10 | 0.1 |
| 合计 | 100 | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com