
| 3 |
| OP |
| OA |
| OB |
| A、[3,9] |
| B、[1,11] |
| C、[6,18] |
| D、[2,22] |
| 3 |
| OP |
| OA |
| OB |
| OP |
| OD |
| OP |
| OA |
| OB |
| 3 |
| 3 |
| OP |
| OA |
| OB |
| OP |
| OD |
| 3 |
| 5 |
| 4 |
| 5 |
| OP |
| OA |
| OB |
| OP |
| OA |
| OB |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| c |
| z | 2 1 |
| z | 2 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、奇函数 |
| B、偶函数 |
| C、奇函数或偶函数 |
| D、可能既不是奇函数,也不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
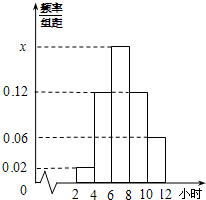 某校为了解学生寒假期间的学习情况,从初中及高中各班共抽取了50名学生,对他们每天平均学习时间进行统计.请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题:
某校为了解学生寒假期间的学习情况,从初中及高中各班共抽取了50名学生,对他们每天平均学习时间进行统计.请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题:| 年级 | 人数 |
| 初一 | 4 |
| 初二 | 4 |
| 初三 | 6 |
| 高一 | 12 |
| 高二 | 6 |
| 高三 | 18 |
| 合计 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com