
【题目】已知函数f(x)=ax2+2x+c,若不等式f(x)<0的解集是{x|-4<x<2}.
(1)求f(x)的解析式;
(2)判断f(x)在(0,+∞)上的单调性,并用定义证明;
(3)若函数f(x)在区间[m,m+2]上的最小值为-5,求实数m的值.
【答案】(1)![]() (2)单调递增,证明见解析(3)1或5
(2)单调递增,证明见解析(3)1或5
【解析】
利用二次函数小于零的解集,可以判断-4,2时f(x)=0的解,利用韦达定理,可求得a,c的值;根据单调性定义法(1.取值,2作差,3定号,4下结论),证明函数的单调性;利用函数的单调性确定函数最小值,从而求得m值
因为不等式f(x)<0的解集是{x|-4<x<2}.所以-4,2方程ax2+2x+c=0的两个是根,利用韦达定理:![]() ,解的:a=1,c=-8;故:
,解的:a=1,c=-8;故:![]()
任取![]()
则f(x1)-f(x2)=(x12+2x1-8)-(x22+2x2-8)=(x21- x22)+ 2(x1-x2)
=(x1+x2)(x1-x2)+ 2(x1-x2)=(x1-x2)(x1+x2+2)
因为:![]()
所以:x1-x2<0,x1+x2+2>0,故:f(x1)-f(x2)<0,因此:f(x1)<f(x2)
所以: f(x)在(0,+∞)上为单调递增函数
(3)由(1)知:![]() ,对称轴:x=-1,
,对称轴:x=-1, ![]()
因为函数f(x)在区间[m,m+2]上的最小值为-5,故对称轴落在区间[m,m+2]中,
由于f(x)在区间![]()
当m>-1时,f(x)在区间[m,m+2]上为递增,则最小值![]()
解得:m=-3(舍),m=1
当m<-3时,f(x)在区间[m,m+2]上为递减,
则最小值![]() ,
,
解得:m=-5或m=-1(舍)
故:答案为:m=1或m=-5


 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】对定义域为D的函数,若存在距离为d的两条平行直线![]() 和
和![]() .使得当
.使得当![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 有一个宽度为d的通道有下列函数:(1)
有一个宽度为d的通道有下列函数:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .其中在
.其中在![]() 上通道宽度为1的函数是( )
上通道宽度为1的函数是( )
A. (1)(3) B. (2)(3) C. (1)(3)(4) D. (2)(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为![]() 的水轮绕着圆心
的水轮绕着圆心![]() 逆时针做匀速圆周运动,每分钟转动
逆时针做匀速圆周运动,每分钟转动![]() 圈,水轮圆心
圈,水轮圆心![]() 距离水面
距离水面![]() ,如果当水轮上点
,如果当水轮上点![]() 从离开水面的时刻(
从离开水面的时刻(![]() )开始计算时间.
)开始计算时间.
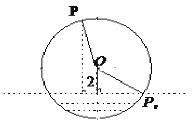
(1)试建立适当的平面直角坐标系,求点![]() 距离水面的高度
距离水面的高度![]() (
(![]() )与时间
)与时间![]() (
(![]() )满足的函数关系;
)满足的函数关系;
(2)求点![]() 第一次到达最高点需要的时间.
第一次到达最高点需要的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 恒成立,则称
恒成立,则称![]() 为
为![]() 的一个上界函数,当(1)中的
的一个上界函数,当(1)中的![]() 为函数
为函数![]() 的一个上界函数时,求
的一个上界函数时,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,对(1)中的
时,对(1)中的![]() ,讨论
,讨论![]() 在区间
在区间![]() 上极值点的个数.
上极值点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】旅行社为某旅行团包飞机去旅游,其中旅行社的包机费为![]() 元.旅行团中的每个人的飞机票按以下方式与旅行社结算:若旅行团的人数不超过
元.旅行团中的每个人的飞机票按以下方式与旅行社结算:若旅行团的人数不超过![]() 人时,飞机票每张
人时,飞机票每张![]() 元;若旅行团的人数多于
元;若旅行团的人数多于![]() 人时,则予以优惠,每多
人时,则予以优惠,每多![]() 人,每个人的机票费减少
人,每个人的机票费减少![]() 元,但旅行团的人数最多不超过
元,但旅行团的人数最多不超过![]() 人.设旅行团的人数为
人.设旅行团的人数为![]() 人,飞机票价格
人,飞机票价格![]() 元,旅行社的利润为
元,旅行社的利润为![]() 元.
元.
(1)写出每张飞机票价格![]() 元与旅行团人数
元与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)当旅行团人数![]() 为多少时,旅行社可获得最大利润?求出最大利润.
为多少时,旅行社可获得最大利润?求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿基米德(公元前287年—公元前212年),伟大的古希腊哲学家、数学家和物理学家,他死后的墓碑上刻着一个“圆柱容球”的立体几何图形,为纪念他发现“圆柱内切球的体积是圆柱体积的![]() ,且球的表面积也是圆柱表面积的
,且球的表面积也是圆柱表面积的![]() ”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为
”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为![]() ,则该圆柱的内切球体积为( )
,则该圆柱的内切球体积为( )
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() , 离心率为
, 离心率为![]() ,左右焦点分别为
,左右焦点分别为![]() , 过点
, 过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆C的方程;
(2)当![]() 的面积为
的面积为![]() 时, 求以
时, 求以![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆的方程.
相切的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com