
点A、B、C、D在同一个球的球面上,AB=BC=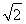 ,AC=2,若四面体ABCD体积的最大值为
,AC=2,若四面体ABCD体积的最大值为 ,则这个球的表面积为( )
,则这个球的表面积为( )
A. B.8π C.
B.8π C. D.
D.
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷1练习卷(解析版) 题型:解答题
为了解某市民众对政府出台楼市限购令的情况,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频数分布及对楼市限购令赞成的人数如下表:
月收入 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
将月收入不低于55的人群称为“高收入族”,月收入低于55的人群称为“非高收入族”.
(1)根据已知条件完成下面的2×2列联表,问能否在犯错误的概率不超过0.01的前提下认为非高收入族赞成楼市限购令?
| 非高收入族 | 高收入族 | 合计 |
赞成 |
|
|
|
不赞成 |
|
|
|
合计 |
|
|
|
(2)现从月收入在[15,25)的人群中随机抽取两人,求所抽取的两人都赞成楼市限购令的概率.
附:K2=
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:解答题
已知双曲线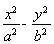 =1(a>0,b>0)的右焦点为F(c,0).
=1(a>0,b>0)的右焦点为F(c,0).
(1)若双曲线的一条渐近线方程为y=x且c=2,求双曲线的方程;
(2)以原点O为圆心,c为半径作圆,该圆与双曲线在第一象限的交点为A,过A作圆的切线,斜率为- ,求双曲线的离心率.
,求双曲线的离心率.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
已知双曲线 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.y=± x B.y=±
x B.y=± x C.y=±2x D.y=±
x C.y=±2x D.y=± x
x
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:解答题
如图,在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC,AB⊥BC,O为AC中点.
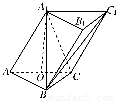
(1)证明:A1O⊥平面ABC;
(2)若E是线段A1B上一点,且满足VE-BCC1=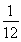 ·VABC-A1B1C1,求A1E的长度.
·VABC-A1B1C1,求A1E的长度.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:选择题
设直线m与平面α相交但不垂直,则下列说法中正确的是( )
A.在平面α内有且只有一条直线与直线m垂直
B.过直线m有且只有一个平面与平面α垂直
C.与直线m垂直的直线不可能与平面α平行
D.与直线m平行的平面不可能与平面α垂直
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:解答题
已知等比数列{an}满足an+1+an=9·2n-1,n∈N*.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,若不等式Sn>kan-2对一切n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:选择题
等比数列x,3x+3,6x+6,…的第四项等于( )
A.-24 B.0 C.12 D.24
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:选择题
下列函数中,与函数y=-3|x|的奇偶性相同,且在(-∞,0)上单调性也相同的是( )
A.y=-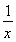 B.y=log2|x|
B.y=log2|x|
C.y=1-x2 D.y=x3-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com