
| A. | (-1,1) | B. | (-1,+∞) | C. | (-∞,-1) | D. | (-∞,+∞) |
分析 可设F(x)=f(x)-(2x+3),从而只要求F(x)>0的解集即可:求导数,并且可得到F′(x)>0,这样F(x)在R上单调递增,根据条件可求出F(-1)=0,从而得出F(x)>0时,便有x>-1,这样即可得出原不等式的解集.
解答 解:设F(x)=f(x)-(2x+3),则F′(x)=f′(x)-2;
∵f′(x)>2在R上恒成立;
∴F′(x)>0在R上恒成立;
∴F(x)在R上单调递增;
又F(-1)=f(-1)-1=1-1=0;
∴F(x)>0的解集为(-1,+∞);
∴f(x)>2x+3的解集为(-1,+∞).
故选:B.
点评 考查构造函数解决问题的方法,根据导数符号判断单调性的方法,以及函数单调性定义的运用.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
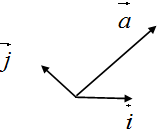 如图,在同一平面内,向量$\overrightarrow a$与单位向量$\overrightarrow i、\overrightarrow j$的夹角分别为30°、90°,已知$|\overrightarrow a|$=$2\sqrt{3}$
如图,在同一平面内,向量$\overrightarrow a$与单位向量$\overrightarrow i、\overrightarrow j$的夹角分别为30°、90°,已知$|\overrightarrow a|$=$2\sqrt{3}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f:x→y=$\frac{1}{2}$x | B. | f:x→y=2x | C. | f:x→y=$\frac{1}{3}$x | D. | f:x→y=x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com