
已知几何体 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.

(1)求此几何体的体积 的大小;
的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)求二面角A-ED-B的正弦值.
(1)16;(2)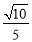 ;(3)
;(3)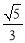 .
.
【解析】
试题分析:(1)由三视图易得AC⊥平面BCE,则体积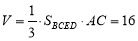 ;(2)取EC的中点是F,连结BF,可证∠FBA或其补角即为异面直线DE与AB所成的角,在△BAF中,利用余弦定理可求得异面直线DE与AB所成的角的余弦值为
;(2)取EC的中点是F,连结BF,可证∠FBA或其补角即为异面直线DE与AB所成的角,在△BAF中,利用余弦定理可求得异面直线DE与AB所成的角的余弦值为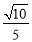 ;(3)过C作CG⊥DE交DE于G,连AG,可证DE⊥平面ACG,
;(3)过C作CG⊥DE交DE于G,连AG,可证DE⊥平面ACG,
易知∠AGC为二面角A-ED-B的平面角,在△ACG中,可求得二面角A-ED-B的的正弦值为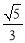 .
.
试题解析:(1)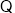 AC⊥平面BCE, 则
AC⊥平面BCE, 则 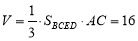
∴几何体的体积V为16.
(2)取EC的中点是F,连结BF,则BF//DE,∴∠FBA或其补角即为异面直线DE与AB所成的角.
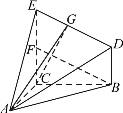
在△BAF中,AB=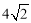 ,BF=AF=
,BF=AF=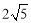 .∴
.∴
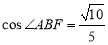 .
.
∴异面直线DE与AB所成的角的余弦值为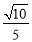
(3)AC⊥平面BCE,过C作CG⊥DE交DE于G,连AG.可得DE⊥平面ACG,
从而AG⊥DE,∴∠AGC为二面角A-ED-B的平面角.
在△ACG中,∠ACG=90°,AC=4,CG=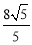 ,∴
,∴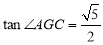 .∴
.∴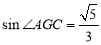 .
.
∴二面角A-ED-B的的正弦值为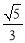 .
.
考点:1.空间几何体的结构特征与三视图;2.空间几何中的线面角与二面角


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2016届福建省高一下学期期中考试数学试卷(解析版) 题型:选择题
某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件、80件、60件.为了解它们的产品质量是否存在显著差别,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n=( )
A.9 B.10 C.12 D.13

查看答案和解析>>
科目:高中数学 来源:2016届福建省泉州市高一下学期期末考试数学试卷(解析版) 题型:选择题
.如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )
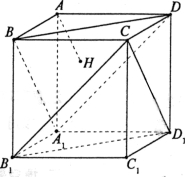
A.点H是△A1BD的垂心
B.AH垂直平面CB1D1[
C.直线AH和BB1所成角为45°
D.AH的延长线经过点C1
查看答案和解析>>
科目:高中数学 来源:2016届湖北省荆门市高一下学期期末质量检测数学试卷(解析版) 题型:填空题
设 ,则
,则 为
为 的调和平均数.如图,
的调和平均数.如图, 为线段
为线段 上的点,
上的点, ,
, ,
, 为
为 的中点,以
的中点,以 为直径作半圆.过点
为直径作半圆.过点 作
作 的垂线交半圆于
的垂线交半圆于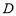 ,连结
,连结 .过点
.过点 作
作 的垂线,垂足为
的垂线,垂足为 .则图中线段
.则图中线段 的长度为
的长度为 的算术平均数,线段 的长度是
的算术平均数,线段 的长度是 的几何平均数,线段 的长度是
的几何平均数,线段 的长度是 的调和平均数.
的调和平均数.
查看答案和解析>>
科目:高中数学 来源:2016届湖北省荆门市高一下学期期末质量检测数学试卷(解析版) 题型:选择题
襄荆高速公路连接襄阳、荆门、荆州三市,全长约188公里,是湖北省大三角经济主骨架的干线公路之一.若某汽车从进入该高速公路后以不低于60千米/时且不高于120千米/时的速度匀速行驶,已知该汽车每小时的运输成本由固定部分和可变部分组成,固定部分为200元,可变部分与速度v(千米/时)的平方成正比(比例系数记为k).当汽车以最快速度行驶时,每小时的运输成本为488元.若使汽车的全程运输成本最低,其速度为
A.80 km /小时 B.90 km /小时 C.100 km /小时 D.110 km /小时
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版必修四 1.1周期现象练习卷(解析版) 题型:选择题
已知角α的终边与单位圆相交于点P(sin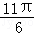 ,cos
,cos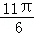 ),则sinα=( )
),则sinα=( )
A.﹣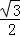 B.﹣
B.﹣ C.
C. D.
D.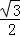
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com